Spectroscopic Applications: |
In Raman spectroscopy, in addition to the incident beam of frequency 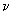 i, the scattered beam contains frequencies i, the scattered beam contains frequencies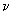 i i 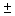 n n 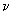 M where n = integer and M where n = integer and 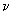 M is the molecular excitation energy. The monochromaticity of laser light allows for easy identification of these closely spaced frequencies. Since the laser beam can be collimated over long paths, the above spread in frequencies can even be detected in the direction of the incident beam itself, which is not possible in Raman spectroscopy with ordinary light. M is the molecular excitation energy. The monochromaticity of laser light allows for easy identification of these closely spaced frequencies. Since the laser beam can be collimated over long paths, the above spread in frequencies can even be detected in the direction of the incident beam itself, which is not possible in Raman spectroscopy with ordinary light. |
| One of the major problems in spectroscopy is the noise of the detector and the interference caused by the background radiation. When these interferences are more than a few percent of the intensity of the absorbing light it is difficult to distinguish between signals and noise. Since the laser beams have high intensity, the laser light is particularly useful in measuring the intensities of the scattered light. This is a major advantage in Raman spectroscopy which studies frequencies of scattered radiation. |
|
|
The high power of the laser beam also allows one to precisely locate the absorption maxima, which could be rather broad when laser light is not used. Another area of spectroscopy that has grown with lasers is multiphoton spectroscopy. Normal selection rules use only the linear terms in the electric field in transitions allowed by the transition dipole moment. The linear term in the transition in the dipole moment is
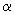 E (where E (where
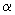 = polarizability and E is the electric field). = polarizability and E is the electric field). |
| |
When the light intensity is very high, the non-linear terms like
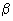 E2 begin to contribute. The electric field is expressed as E0 cos(wt). The square of the electric field contains terms such as cos (2wt) (recall that cos2wt = 1/2 (1 + cos 2wt) and thus two photons of frequency w can cause a transition with frequency 2w in a molecule (under intense laser radiation). This is called multiphoton spectroscopy. Transitions that are disallowed in ordinary spectroscopy become accessible in multiphoton spectroscopy. E2 begin to contribute. The electric field is expressed as E0 cos(wt). The square of the electric field contains terms such as cos (2wt) (recall that cos2wt = 1/2 (1 + cos 2wt) and thus two photons of frequency w can cause a transition with frequency 2w in a molecule (under intense laser radiation). This is called multiphoton spectroscopy. Transitions that are disallowed in ordinary spectroscopy become accessible in multiphoton spectroscopy. |
| |
We know that reaction rates can be increased by increasing the temperature. But increasing the temperature increases the energies of not only the relevant molecules, but all molecules. For example, the reaction BCl3 + C6H6 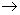 C6H5 - BCl2 + HCl occurs with significant rates only above 600oC and in the presence of a catalyst. But with a laser light of 10.6 C6H5 - BCl2 + HCl occurs with significant rates only above 600oC and in the presence of a catalyst. But with a laser light of 10.6
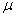 m of a CO2 laser, the reaction occurs at room temperature without a catalyst. The reason for this is that with the laser light, one is able to excite the relevant vibrations/excitations selectively! Thus, if low cost laser beams are available, a lot of reactions can be carried out with state selectivity and many compounds which are unstable at high temperatures can be made at room temperature. m of a CO2 laser, the reaction occurs at room temperature without a catalyst. The reason for this is that with the laser light, one is able to excite the relevant vibrations/excitations selectively! Thus, if low cost laser beams are available, a lot of reactions can be carried out with state selectivity and many compounds which are unstable at high temperatures can be made at room temperature. |
| |