Let r be the radius of the smaller inner sphere and let R be the radius of the outer sphere. Then, |
| R / ( R +r ) = cos ( 30o ) = 0.866 |
(17.5) |
|
| and the critical radius ratio r / R = 0.155 |
(17.6) |
| For tetrahedral coordination, two spheres of radius R and the smaller one of radius r are shown in fig 17.6 (b). The other two spheres of radius R lie above and below the plane of the figure, with the four spheres of radius R equidistant from the central point O.
|
| The tetrahedral angle is 109o 28' and is indicated in Fig 17.6 (b) |
| |
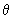 = 90 - (109o 28')/2 = 35 o16' = 90 - (109o 28')/2 = 35 o16' |
(17.7) |
| |
| and cos ( 35o 16' ) = R / ( R + r ) |
(17.8) |
| |
| r/ R = 0.255 |
(17.9) |
| The case of octahedral coordination is shown in Fig 17.6 ( c ). In this case, |
| |
| cos 45o = R / ( r + R ) and r / R = 0.414 |
(17.10) |
| In this manner, we can evaluate the critical radius ratios for all other coordinations. In Table 17.1, examples for different radius ratios have been given. In ionic crystals cations and anions pack as closely as possible to maximize the Coulombic interaction. Anions always remain farther than what their ionic radii would permit and the cations try to be surrounded by as many anions as possible around them within the permitted radius ratios. For example, if the radius ratio is 0.35, octahedral coordination is ruled out, because, for closest packing, the anions have to be closer than that permitted by the sum of their radii and hence tetrahedral coordination prevails. |
| |
Range of Radius Ratios |
Geometries |
Coordination numbers |
Examples of solids |
Central Cation |
0
 0.155 |
linear |
2 |
HF |
H+ |
0.155  0.225 |
triangular |
3 |
BO3 |
B3+ |
0.225  0.414 |
tetrahedral |
4 |
SiO2 |
Si4+ |
0.414 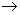 0.712 |
octahedral |
6 |
MgO2 |
Mg2+ |
0.712 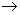 1 |
cubic |
8 |
CsCl |
Cs+ |
|
| |
Table 17.1 Radius ratios, geometries and coordination numbers. |
| |