12.4 |
Electronic Spectroscopy of Atoms
|
| |
For hydrogen atom, the selection rules (the rules that govern whether a transition is allowed or not) are
∆n = any integer
∆l = ± 1 (12.9)
The consequences of these conditions are that all transitions from 1s → np (n ≥ 2) are allowed. Similarly 2p → 3s, 2p → 3d, 2p → 1s, 3s → 4p, ….. are all allowed transitions. In Equation (12.9), n is the principal quantum number. The well known Lyman series arises from the transions from the n = 1 state to n´ = 2, 3,4,5… The Balmer series arise from the transitions from the n = 2 state to n´ = 3,4,5…. The other series named after Paschen (n = 3), Brackett (n = 4) and Pfund (n = 5) can be readily rationalized. The formula for ∆E is the well known Bohr’s formula.
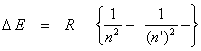 (12.10) (12.10)
Where n is the initial quantum number and n’, is the number or state resulting from the absorption of radiation. The Rydberg constant R = 109677.581 cm-1
We have already studied that for each angular momentum L, there are (2 l + 1) values of ml. The values of ml correspond to the projection of the angular momentum vector L in different directions. In the same manner, the spin angular momentum vector s can also be projected in (2s + 1) = 2 directions. The projections are pictorially shown in Fig. 12.4.
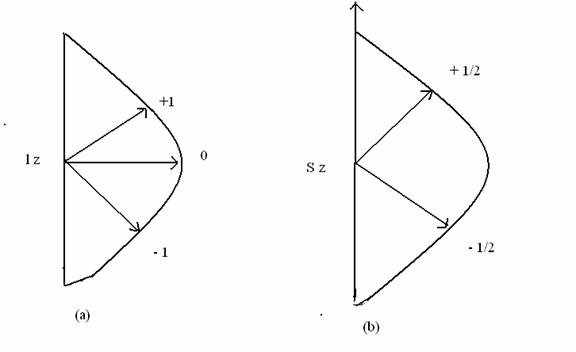
Fig. 12.4 Projections of L and S along the z – axis. The lz values of 1, 0, -1 are shown in (a) and sz = ˝ and - ˝ are shown in (b).
The magnitude of orbital angular momentum L is given by √ [l (l + 1)] ћ, where ћ = h/2π.
Due to the interaction of these two angular momenta, additional states result and the spectral lines get split into doublets and multiples. New selection rules have to be written in terms of the total angular momentum quantum number J which is defined as
J = L + S (12.11)
The addition of these angular momenta are governed by special vector addition rules. The values of J and L + S are L – S. For each value of J (with a corresponding magnitude of angular momentum = √ [j (j + 1)] ћ ) there are 2j + 1 projections similar to the ones in Fig. 12.4. The new selection rules are
∆ n = any integer (12.12)
∆j = 0, ± 1
∆l = ± 1
With the introduction of the total angular momentum, a state is associated with a term symbol.
(2s + 1)L J (12.13)
Where (2s + 1) is the spin multiplicity, L = magnitude of orbital angular momentum and J is the total angular momentum. With the new selection rules, the earlier S → P transition which was a single line, now gets split into two lines as follows
2S1/2 → 2P1/2 (∆j = 0)
2S1/2 → 2P3/2 (∆j = +1)
(12.14)
This splitting of lines is called the fine structure of spectral lines.
In the case of many electron atoms, the degeneracy of 2s and 2p and 3s, 3p and 3d which was present in the H – atom, ceases to exist and the orbital energies are ordered as
1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d (12.15)
The filling up on electrons in atoms is done by using the Pauli’s exclusion principle and the Hund’s rule. According to Hund’s rules, states with higher multiplicity are favored, ie., electrons occupy degenerate orbitals in such a way as to keep their spins parallel.
The spectra of He+, Be+, B2+ which have single electron outside a closed shell show spectra similar to hydrogen. They are referred to as ‘hydrogen-like spectra’. In Lithium, the 2S1/2 → n2P1/2, 3/2 part of the spectrum is similar to hydrogen, but the lines arising from the 2p states form compound doublets as shown below
2 2P1/2, 3/2 → n 2S1/2 (12.16a)
2 2P1/2, 3/2 → n 2D3/2, 5/2 (12.16b)
When the ground state of an atom has more than one unpaired electron as in the case of carbon, the spectra show a lot of complexity in their structure.
|