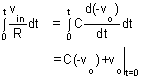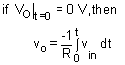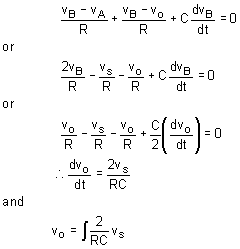Integrator:
A circuit in which the output voltage waveform is the integral of the input voltage waveform is called integrator. Fig. 4, shows an integrator circuit using OPAMP.
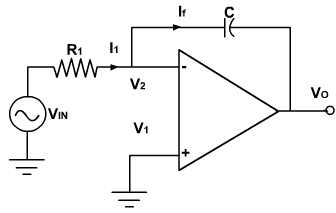
Fig. 4
Here, the feedback element is a capacitor. The current drawn by OPAMP is zero and also the V2 is virtually grounded.
Therefore, i1 = if and v2 = v1 = 0
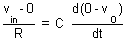
Integrating both sides with respect to time from 0 to t, we get
The output voltage is directly proportional to the negative integral of the input voltage and inversely proportional to the time constant RC.
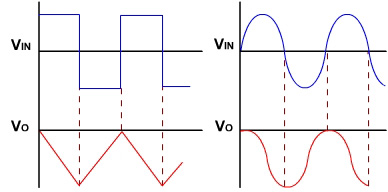
If the input is a sine wave the output will be cosine wave. If the input is a square wave, the output will be a triangular wave. For accurate integration, the time period of the input signal T must be longer than or equal to RC.
Fig. 5, shows the output of integrator for square and sinusoidal inputs.
Fig. 5
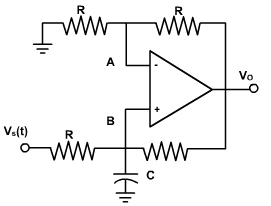
Example - 3
Prove that the network shown in fig. 6 is a non-inverting integrator with
.
Solution:
The voltage at point A is vO / 2 and it is also the voltage at point B because different input voltage is negligible.
vB = VO / 2
Therefore, applying Node current equation at point B,
Fig. 6