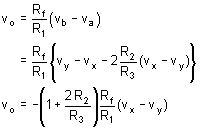Example - 1

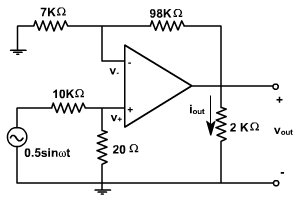
Find v_out and i_out for the circuit shown in fig. 2. The input voltage is sinusoidal with amplitude of 0.5 V.

Fig. 2

Solution:

We begin by writing the KCL equations at both the + and – terminals of the op-amp.

For the negative terminal,

Therefore,

15 v_- = v_out

For the positive terminal,

This yields two equations in three unknowns, v_out, v₊ and v_-. The third equation is the relationship between v₊ and v_- for the ideal OPAMP,

v₊ = v_-

Solving these equations, we find

v_out = 10 v_in = 5 sinωt V

Since 2 kΩ resistor forms the load of the op-amp, then the current i_out is given by

Example - 2

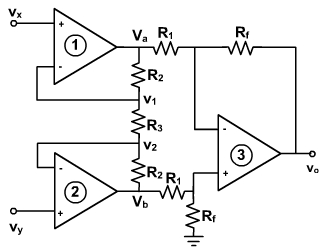
For the different amplifier shown in fig. 3, verify that

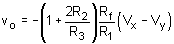
Fig. 3

Solution:

Since the differential input voltage of OPAMP is negligible, therefore,

v₁= v_x
and v₂ = v_y

The input impedance of OPAMP is very large and, therefore, the input current of OPAMP is negligible.

Thus
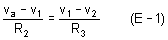
And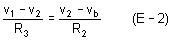
From equation (E-1)

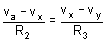
or       

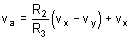
From equation (E-2)

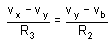
or       

The OPAMP3 is working as differential amplifier, therefore,

GOTO >> 1 || 2 || 3 || Home