Finite Potential well
U(x) = U 0 otherwise
We assume a particle with energy 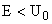 confined to the potential well confined to the potential well
For 0 < x < a,
For x <0,
For x > 0,
The three sets of solution are
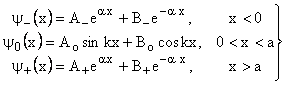 .....(1) .....(1)
|
|
Now we set up the boundary conditions.
Far from the potential well, wave functions must go to zero as the probability of finding the particle away from potential region = 0
Therefore, 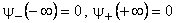
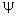 must be continuous at well boundary must be continuous at well boundary
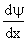 must be continuous at well boundaries x = 0 & x = a must be continuous at well boundaries x = 0 & x = a
From boundary conditions 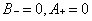
And we get four simultaneous equations
elimination 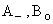 and and 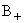 we obtain we obtain
if 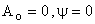 identically. identically.
Therefore, 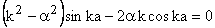
or
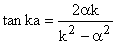
This is a transcendental equation
We define a dimensionless quantity
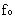 is constant of the system. is constant of the system.
and
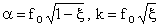 from definition of k & from definition of k & 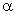 . .
Eigen value equation becomes
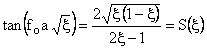
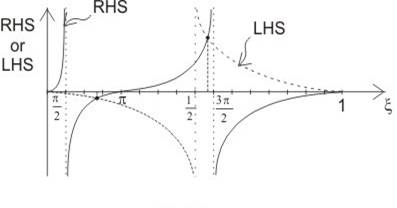
|
Fig. 2.6 |
Let 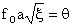 then then
if 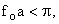 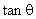 intersect intersect 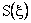 at one points at one points
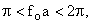 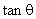 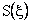 intersect at 2 points intersect at 2 points
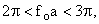 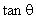 intersect intersect 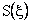 at 3 points at 3 points
So for,
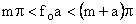 there are m points. there are m points.
In the limit 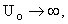 (E finite). (E finite). 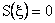 . .
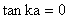
Finite potential
In finite potential wells, we talked about Eigen value equation
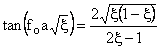 (1) (1)
|
for a given system constant
We have a discrete no. of solutions where LHS or RHS of (1) intersect.
|
Fig.2.7 |
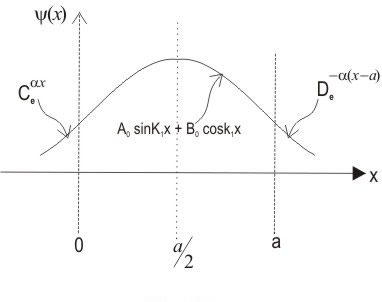
Wave Function of Finite Potential Wells
For each intersection a value of 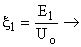 particular particular 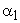 and and 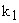
 outside the well of potential outside the well of potential
One can clearly see from this that there is a finite probability of existence outside in the classically forbidden region (classically a particle with an energy 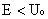 cannot exist outside the well). If the potential well is slightly modified as in the figure below. cannot exist outside the well). If the potential well is slightly modified as in the figure below.
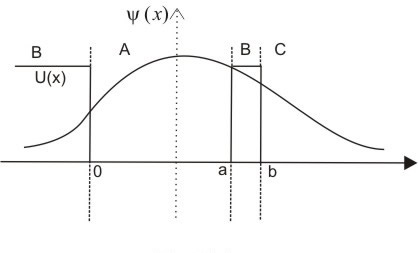
|
Fig.2.8 |
The wave function will be nonzero in region C also.
Thus the particle will have a finite probability of existing or coming in region C past the potential barrier B
In C the particle can appear as a free particle.
This quantum mechanical phenomenon of passing through a barrier is known as tunneling. The wave function is different inside and outside.
Therefore there exists a finite probability of reflection at the well walls, called quantum mechanical reflection at the well walls. In analogy to optics it may be looked at as two partially reflecting mirrors, where an infinite potential well could be visualized as two 100% reflecting mirrors.
It is used in Tunnel diodes and operation of many other solid-state devices. One of the usage of this phenomenon for high frequency decive is called Resonant Tunnelling Diode (RTD), which would be used as an oscillator and even as an amplifier.
|