Particle in an infinite potential well
Particle of mass m and fixed total energy E confined to a relatively small segment of one dimensional space between x = 0 and x = a. In terms of the potential energy we can view that the particle is trapped in an infinitely deep one dimensional potential well with 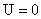 constant for 0 < x < a constant for 0 < x < a
Now time independent Schrödinger equation is
Boundary conditions
Solving 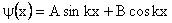 which can also be represented as which can also be represented as
A + exp (+jkx) + A - exp (-jkx) |
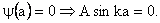
Since 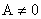 , as , as 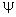 vanishes for all x, so vanishes for all x, so
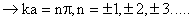 discrete values. discrete values.
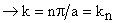
Therefore, 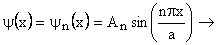 modes or eigen functions modes or eigen functions
for 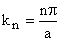 , Energy , Energy 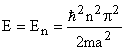
So particle can have only a few discrete energy states/levels
Wave function 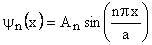
 standing wave standing wave
 particle is bouncing back and forth between the walls of the potential well. particle is bouncing back and forth between the walls of the potential well.
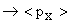 average value of momentum at any x is 0. So to calculate momentum we have to isolate forward wave going in +x or backward wave going in -x. average value of momentum at any x is 0. So to calculate momentum we have to isolate forward wave going in +x or backward wave going in -x.
For +x wave, 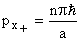 and -x going wave and -x going wave 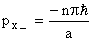 Discrete Discrete 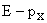 points lie on the continuous points lie on the continuous 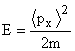 parabola of a free particle. parabola of a free particle.
The integer n is called the quantum number
Value of 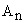 from the equation that from the equation that 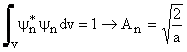
|