Solution of Schrödinger Equation
Free Particle
A particle (electron), alone in the universe.
Particle  mass m and a fixed total energy E. mass m and a fixed total energy E.
Alone  no force on the particle. no force on the particle.
 constant potential energy everywhere constant potential energy everywhere
U(x, y, z) = constant, say zero
Let universe = one Dimensional only x variation 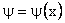
Time independent Schrödinger equation 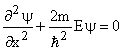
which can be written as 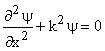 , a one dimensional differential equation.Where , a one dimensional differential equation.Where 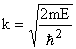 or or 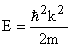 or E has a parabolic dependence on k. General solution for the simple equation can be written as or E has a parabolic dependence on k. General solution for the simple equation can be written as 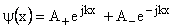 where where 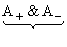 are unknown constants. are unknown constants.
Therefore, total wave function (space and time dependence)
Compare this with a time-harmonic electromagnetic wave in free-space where
k = constant of propagation = 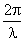
Hence wave function of free particle consists of a traveling wave. If particle moves in+x then 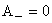 and and 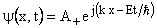
Where 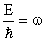
Normalizing, 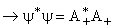 = constant for all values of x. = constant for all values of x.
Thus the probability of finding the particle in any dx is equal/same
If we take the universe to be infinite 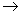 Probability = 0 Probability = 0
If we take the universe to be finite but large
 no such difficulty no such difficulty
Now momentum  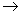 operator = operator = 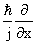
Therefore, expected value of momentum
Same as classical. Therefore, 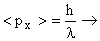 DeBroglie relationship DeBroglie relationship
|