LINEAR HARMONIC OSCILLATOR
A harmonic oscillator is a particle which is bound to an equilibrium position by a force which is proportional to the displacement from that position.
Thus we have,
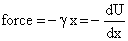
|
(1) |
where 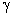 is the spring constant. is the spring constant.
The potential is expressed as,
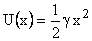
|
(2) |
The linear harmonic oscillator can then be visualized on a mass connected to a spring of spring constant 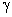 on shown in Fig. 2.8 on shown in Fig. 2.8
The time independent Schrödinger equation is given by,
or,
To solve equation (3), we consider a dimension less quantity,
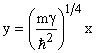
|
(4) |
and
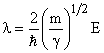
|
(5) |
using (5) and (4)
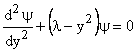
|
(6) |
For large values of y we can neglect 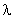 we get equation (6) on, we get equation (6) on,
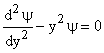
|
(7) |
Equation (7) is satisfied approximately by the solution,
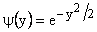
|
(8) |
Substituting equation (8) in (7) we get,
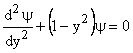
|
(9) |
This indicates that equation (8) satisfied equation (7) approximately and hence we consider the exact solution as,
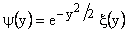
|
(10) |
Putting the value of 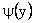 from (10) in (6) from (10) in (6)
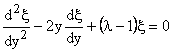
|
(11) |
The trick next, is to linearize the above equation.
Equation (11) can be solved by using the power series method.
Let the trail solution be,

|
(12) |

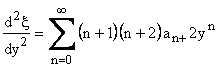
|
(13) |
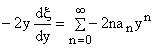
|
(14) |
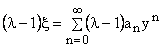
|
(15) |
Putting equation (13), (14) and (15) in (11),
This equation must hold for all values of 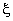 , and therefore the coefficient of each power of , and therefore the coefficient of each power of 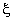 must vanish separately. must vanish separately.
This gives in the recursion relation between 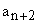 and a n , and a n ,
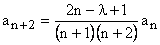
|
(16) |
It seems that knowing 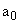 and and 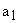 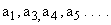 can be calculated by using equation (16), can be calculated by using equation (16),
Thus we can write equation (12) as,
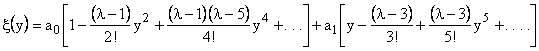
|
(17) |
If in the equation (16) 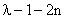 should be zero for some value of the index n, then should be zero for some value of the index n, then 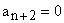 . But since . But since 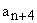 is a multiple of is a multiple of 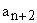 so on, all the succeeding coefficients which are related to so on, all the succeeding coefficients which are related to 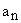 by the recursion relation (16) would vanish, and one or the other bracketed series in equation (17) would terminate to become a polynomial of degree n. by the recursion relation (16) would vanish, and one or the other bracketed series in equation (17) would terminate to become a polynomial of degree n.
This occurs, when,
or, |
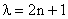
|
(n = 0, 1, 2 ..) |
(18) |
Energy Quantization :
We have obtained the condition when the wave function is acceptable as
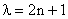 (n = 0, 1, 2 . . .) (n = 0, 1, 2 . . .)
|
again 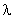 was was 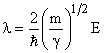
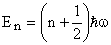
|
(19) |
The variation of the energy levels is shown in the Fig.2.10
Reference:
1. R.F. Pierret, Advanced Semiconductor Fundamentals, ( Volume VI in Modular Series on Solid devices),
Addison Wesley Publishing House Reading , MA , 1989.
2. Solid State and Semiconductor Physics, 2 nd Edn. J.P.Mckelvey, 1966, Harper and Row, New Y
3. Introduction to Solid State Physics, 7 th Edition by C. Kittel (John Wiley & Sons, 1996).
|