Transient response of Diode
The diode will not respond to the reverse voltage until excess minority carriers in neutral n and p regions have been withdrawn.
Model of diode
If we apply reverse bias suddenly then the diode passes a reverse current higher than reverse saturation current 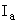 for some t. The current then falls as the stored minority carriers are withdrawn, eventually reaching for some t. The current then falls as the stored minority carriers are withdrawn, eventually reaching 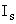 . .
One can use charge storage model to understand this transient behaviour.
Consider a 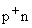 junction-depletion region on the n side then the essential minority carrier is p only. junction-depletion region on the n side then the essential minority carrier is p only.
Fig 10.7 depicts the hole distribution in neutral n-region.
Multiplying continuity equation by qAdx and integrating it over the entire neutral n region from x n to w 1 , we get
which can be written as
where 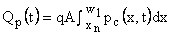 is the excess minority carrier stored in a n region at any time. is the excess minority carrier stored in a n region at any time. 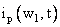 is hole current at x = w 1 and is related to the transit time and neutral n region of width w 1 is hole current at x = w 1 and is related to the transit time and neutral n region of width w 1
A time constant 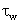 is defined by the relation, is defined by the relation,
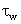 is related to the passage time through the neutral n-region of width W n , so we can write is related to the passage time through the neutral n-region of width W n , so we can write
where
the switching trajectory is shown in Fig. 10.12
Now in storage phase 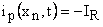 almost constant so the equation almost constant so the equation
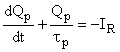 has the solution has the solution
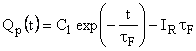
where 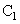 is a constant and is determined by the condition that is a constant and is determined by the condition that
at t = 0 , 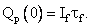
hence 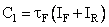
 . .
Now we assume a triangular hole distribution where the charge remains constant in the n-region at 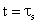 , as depicted in Fig. 10.13 , as depicted in Fig. 10.13
and
where 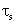 is the time till the diode remains forward biased is the time till the diode remains forward biased
Thus
The stored charge is equal to the area of the triangle with base 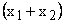 , so , so
writing 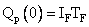 and solving for and solving for 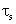 we get we get
Solving
More accurate derivation of 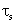 involves solution of time-dependent continuity equation with appropriate boundary conditions and is given as involves solution of time-dependent continuity equation with appropriate boundary conditions and is given as
|