Varactor application
Varactor voltage 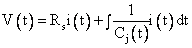 , where i(t) is the current flowing, where, , where i(t) is the current flowing, where, 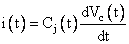
This is difficult to solve and therefore the analysis is done in the frequency domain where a set of coupled non-linear algebraic equation are solved. In this case
and
where m and n are harmonic numbers and P m,n is the average power flowing into non-linear harmonics n 
An important application of pumped varactors is the parametric amplifier. When the varactor is pumped at a frequency F p and a signal is introduced as F c then at F s the varactor behaves as an impedance with a negative real parts. The negative part can be used for amplification. The series resistance limits the frequencies F p and F s and introduces noise.
For losses reactances the power is
Therefore the Manley-Rowe frequency-power formula for the case of lossless reactance are
The output voltage is
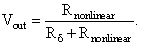 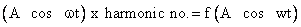
If the parametric amplifier is designed such that only power can flow at input frequency 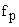 and output frequency is available at nF p and output frequency is available at nF p
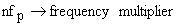 , frequency dividers, rational fraction generators. Hence , frequency dividers, rational fraction generators. Hence
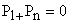 , P 1 corresponds to power at f p . , P 1 corresponds to power at f p .
Parametric small signal amplifiers and frequency converters
If the RF signal at frequency 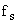 is small compared to pump signal at frequency is small compared to pump signal at frequency 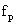 , the power exchanged at the side band frequencies , the power exchanged at the side band frequencies 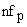 and and 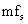 for for 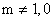 is negligible. is negligible.
Thecorresponding Manley-Rowe equation is
Under this condition the optimum gain is
where,
 is the modulation ratio, f c is the dynamic cut-off frequency given by is the modulation ratio, f c is the dynamic cut-off frequency given by
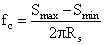 , R s being the series resistance and S max -S min is the elastance swing , R s being the series resistance and S max -S min is the elastance swing
|