For 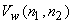 which is zero mean and uncorrected with which is zero mean and uncorrected with 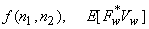 and and 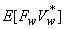 are zero and an estimate of are zero and an estimate of 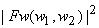 is obtained as is obtained as
where 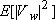 obtained from known or measured properties of obtained from known or measured properties of 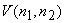
From above estimate 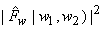 is not guaranteed to be non-negative. To ensure this, is not guaranteed to be non-negative. To ensure this, 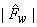 is assured zero if is assured zero if 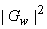 is is 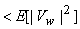
Given an estimate of 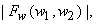 there are many different ways to estimate there are many different ways to estimate 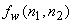 . .
One method that is frequently used and is consistent with the idea that mean square error filters such as Wiener filters are zero phase is to approximate
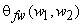 by by 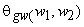 . .
In equation (6.3.2), 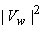 can be viewed as a periodgram and since variance of periodgram is known to be very large subtraction of can be viewed as a periodgram and since variance of periodgram is known to be very large subtraction of 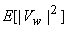 does not reduce noise sufficiently. To reduce more noise at the expense of more signal distortion, does not reduce noise sufficiently. To reduce more noise at the expense of more signal distortion, 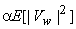 with with 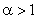 is often subtracted from is often subtracted from 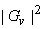 In this case, the estimate In this case, the estimate 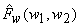 is obtained from is obtained from
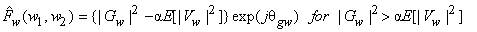 |
(6.3.6) |
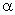 is a parameter that controls the level of noise reduction. is a parameter that controls the level of noise reduction.
Since equation (6.3.6) is used for each subimage and the processed subimages are combined to form the whole image, the method is called "short space" spectral subtraction. This method can be viewed as enhancing the SNR. Since the same function Is subtracted from 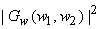 in both high detail and low detail region, the subtraction has a relatively small effect in high detail/region, where in both high detail and low detail region, the subtraction has a relatively small effect in high detail/region, where 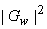 is relatively large. In low detail regions where is relatively large. In low detail regions where 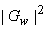 is relatively small & consists primarily of the noise component, the subtraction eliminates a relatively large portion of is relatively small & consists primarily of the noise component, the subtraction eliminates a relatively large portion of 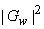 . .
Separable overlapped triangular window is used in this method.
Phase retrieval Method
The algorithm is shown as a flow chart. This also has been observed to converge to the desired solution when the initial estimate used is quite accurate or the signal 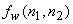 has a special characteristic such as triangular region of support. has a special characteristic such as triangular region of support.
The magnitude only reconstruction problem specifies 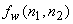 within a sign factor, translation and rotation by within a sign factor, translation and rotation by 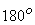 . Hence more than one solution is possible .Imposing an initial estimate sufficiently close to a possible solution or imposing additional constraints such as triangular region of support appear to prevent the iterative process from wandering. . Hence more than one solution is possible .Imposing an initial estimate sufficiently close to a possible solution or imposing additional constraints such as triangular region of support appear to prevent the iterative process from wandering. |