The filters 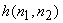 where where 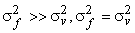 and and 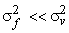 are shown in Fig (6.10) for M=1. We note from Fig (6.10) that are shown in Fig (6.10) for M=1. We note from Fig (6.10) that 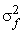 decreases relative to decreases relative to 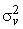 , more noise smoothing is performed. Referring back to fig (6.9), to measure the local signal detail in the system, the algorithm developed uses the signal variance , more noise smoothing is performed. Referring back to fig (6.9), to measure the local signal detail in the system, the algorithm developed uses the signal variance 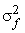 . .
The specific method used to design the space-variant 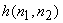 is given by (6.3.3) . is given by (6.3.3) .
This filter is typically a small FIR filter of size say 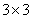 or or 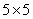 or or 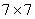 . Hence pixel by pixel processing is employed. Since . Hence pixel by pixel processing is employed. Since 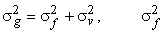 may be estimated from may be estimated from 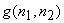 by, by,
| |
if 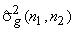 is is 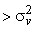 |
The local mean estimate 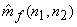 can be obtained from (6.3.2) and can be obtained from (6.3.2) and 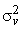 is assumed known. is assumed known.
In the method described above, unlike non-adaptive Wiener filter, the processed image has a significant amount of noise reduction without noticeable blurring.
Figure 6.10 Impulse response of a space-variant image restoration filter as a function of 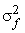 and and 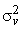 |
Short-Space Spectral Subtraction:
This method to reduce additive noise is a straight forward extension of method developed to reduce additive random noise in speech.
We consider subimage by subimage processing by applying a window 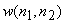 to the degraded image to the degraded image 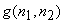 i.e. i.e.
The window is chosen s.t. the subimage 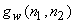 can be assumed approximately stationary. can be assumed approximately stationary.
with 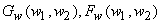 and and 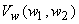 - denoting Fourier Transforms,
we obtain, - denoting Fourier Transforms,
we obtain,
| or, |
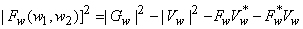 |
|
In this method 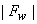 is estimated based on equation (6.3.4) is estimated based on equation (6.3.4)
From the degraded subimage 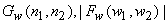 can be obtained directly. can be obtained directly.
The terms 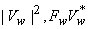 and and 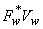 can not be obtained exactly and are approximated by can not be obtained exactly and are approximated by 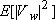 and and 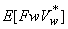 . .
|