Reduction of Image Blurring
An image degraded by blurring can be modeled as
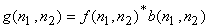 |
(6.4.1) |
In (6.4.1), the degraded image 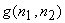 is the result of convolving the original image is the result of convolving the original image 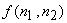 with an impulse response with an impulse response 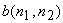 . The sequence . The sequence 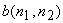 is called the point spared function or the blurring function. The degradation that may be modeled by convolution noise includes blurring due to lens misfocus, motion, and atmospheric turbulence. is called the point spared function or the blurring function. The degradation that may be modeled by convolution noise includes blurring due to lens misfocus, motion, and atmospheric turbulence.
The problem of reducing image blur can be classified into two categories. One is the deconvolution problem, in which 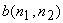 is assumed to be known. The second is the blind deconvolution problem, where is assumed to be known. The second is the blind deconvolution problem, where 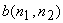 is not known and must be estimated from the available information. In Section 6.4.1, we discuss inverse filtering, a standard approach to solving the deconvolution problem. In section 6.4.2, we discuss algoratirhms developed to solve the blind deconvolution problem. is not known and must be estimated from the available information. In Section 6.4.1, we discuss inverse filtering, a standard approach to solving the deconvolution problem. In section 6.4.2, we discuss algoratirhms developed to solve the blind deconvolution problem.
6.4.1 Inverse Filtering
When the blurring function 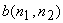 is assumed known, one approach to deblurring is inverse filtering. From (6.4.1) is assumed known, one approach to deblurring is inverse filtering. From (6.4.1)
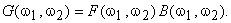 |
(6.4.2) |
From (6.4.2)
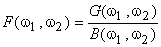 |
(6.4.3) |
From (6.4.3), a system that recovers 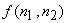 from from 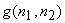 is an inverse filter, shown in Figure 6.11. is an inverse filter, shown in Figure 6.11.
Figure 6.11 Inverse filtering for image restoration |
The inverse filter in Figure 6.11 tends to be very sensitive to noise. When 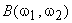 is very small, is very small, 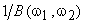 is very large, and small noise in the frequency regions where is very large, and small noise in the frequency regions where 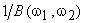 is very large may be greatly emphasized. One method of lessening the noise sensitivity problem is to limit frequency response is very large may be greatly emphasized. One method of lessening the noise sensitivity problem is to limit frequency response
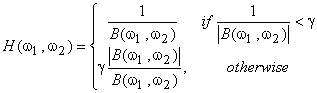 |
(6.4.4) |
The inverse filter 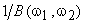 and its variation in (6.3.4) can be implemented in a variety of ways. We may design a filter whose frequency response approximates the desired one, using the standard 2D filter design techniques, and then convolve the blurred image with the designed filter. Alternatively, we can implement the system, using DFTs and inverse DFTs in a manner analogous to the Wiener filter implementation discussed in Section 6.2.1. and its variation in (6.3.4) can be implemented in a variety of ways. We may design a filter whose frequency response approximates the desired one, using the standard 2D filter design techniques, and then convolve the blurred image with the designed filter. Alternatively, we can implement the system, using DFTs and inverse DFTs in a manner analogous to the Wiener filter implementation discussed in Section 6.2.1.
|