Example (Energy compaction and decorrelation ):
Consider
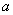 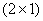 zero mean vector zero mean vector 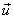 that is unitarily transformed to, that is unitarily transformed to,

where  and and  represents the correlation between represents the correlation between  and and 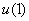 . It is required to find the energy of the transformed coefficients. . It is required to find the energy of the transformed coefficients.
Given
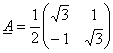 We have
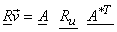
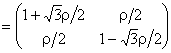
From the matrix

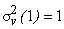
 Total average energy of 2 is distributed equally between Total average energy of 2 is distributed equally between 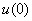 and and  . .
But from 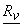 we note , we note ,
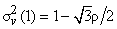 and and 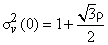 . .
The total average energy is 2, but average energy in  is greater than that in is greater than that in  . .
If  , then , then  of total average energy is packed in first sample. of total average energy is packed in first sample.
Correlation between  and and  is is

Now
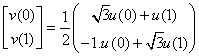
It follows that: 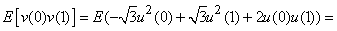 ρ ρ

that is,  is less in absolute value than is less in absolute value than  for for  . .
For 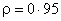 we find we find 
 correlation between transform coefficients has reduced. correlation between transform coefficients has reduced.
|