Discrete Fourier Transform
The discrete Fourier transform (DFT) is "the Fourier transform for finite-length sequences" because, unlike the (discrete-space) Fourier transform, the DFT has a discrete argument and can be stored in a finite number of infinite word-length locations. Yet, it turns out that the DFT can be used to exactly implement convolution for finite-size arrays. Our approach to the DFT will be through the discrete Fourier series DFS, which is made possible by the isomorphism between rectangular periodic and finite-length, rectangular-support sequences. Definition (discrete Fourier transform)
For a finite-support sequence 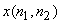 with support with support 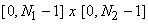 , we define its DFT , we define its DFT
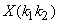 for integers for integers 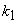 and and 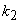 as follows. as follows.
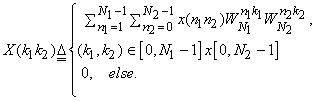 |
(4.2.1) |
Figure(4.1) and Figure( 4.2)
We note that the DFT maps finite support rectangular sequences into themselves. Pictures of the DFT basis functions of size 8 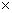 8 are shown with real parts in Figure (4.1) and imaginary parts in Figure (4.2). The real part of the basis functions represent the components of x that are symmetric with respect to the 8 8 are shown with real parts in Figure (4.1) and imaginary parts in Figure (4.2). The real part of the basis functions represent the components of x that are symmetric with respect to the 8 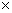 8 square, while the imaginary parts of these basis functions represent the nonsymmetric parts. In these figures, the color white is maximum positive (+1), mid-gray is 0, and black is minimum negative (-1). Each basis function occupies a small square, all of which are then arranged into a 8 8 square, while the imaginary parts of these basis functions represent the nonsymmetric parts. In these figures, the color white is maximum positive (+1), mid-gray is 0, and black is minimum negative (-1). Each basis function occupies a small square, all of which are then arranged into a 8 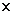 8 mosaic. Note that the highest frequencies are in the middle at 8 mosaic. Note that the highest frequencies are in the middle at
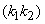 =(4,4) and correspond to the Fourier transform at =(4,4) and correspond to the Fourier transform at
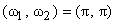 . So the DFT is seen as a projection of the finite-support input sequence x(n1,n2) onto these basis functions. The DFT coefficients then are the representation coefficients for this basis. The inverse DFT (IDFT) exists and is given by . So the DFT is seen as a projection of the finite-support input sequence x(n1,n2) onto these basis functions. The DFT coefficients then are the representation coefficients for this basis. The inverse DFT (IDFT) exists and is given by
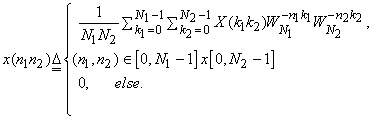 |
(4.2.2) |
The DFT can be seen as a representation for x in terms of the basis functions 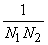 . . 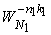 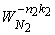 and the expansion coefficients and the expansion coefficients 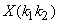 . .
The correctness of this 2-D IDFT formula can be seen in a number of different ways. Perhaps the easiest, at this point, is to realize that the 2-D DFT is a separable transform, and as such, we can realize it as the concatenation of two 1-D DFTs.
Since we can see that the 2-D IDFT is just the inverse of each of these 1-D DFTs in the given order, say row first and then by column, we have the desired result based on the known validity of the 1-D DFT/IDFT transform pair, applied twice.
A second method of proof is to rely on the DFS. The key concept is that rectangular periodic and rectangular finite-support sequences are isomorphic to one another, i.e., given 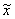 we can define a finite support x as we can define a finite support x as
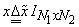 , and given a finite-support x , we can find the corresponding , and given a finite-support x , we can find the corresponding 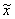 as as
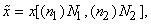 where we use the notation where we use the notation
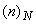 , meaning "n mod N'. Still a third method is to simply insert (1) into (2) and perform the 2-D proof directly. , meaning "n mod N'. Still a third method is to simply insert (1) into (2) and perform the 2-D proof directly.
|