Properties of Unitary transforms :(contd.)
3) Decorrelation :
When input vector elements are highly correlated , the transform coefficients tend to be uncorrelated. That is , the off-diagonal terms of covariance matrix
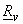 tend to be small compared to diagonal elements. tend to be small compared to diagonal elements. 4) Other properties : (i) The determinant and eigenvalues of a unitary matrix have unity magnitudte.
(ii) Entropy of a random vector is observed under unitary transformation.Since entropy is a measure of average information of the random vector, this means information is preserved under unitary transformation.
Example :
Given the entropy of an 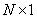 Gaussian random vector Gaussian random vector 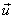 with mean with mean 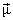 and covariance and covariance 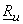 , as : , as :
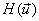 = =
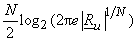
To show 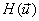 is invariant under any unitary transformation. is invariant under any unitary transformation.
Let 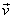 = = 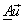
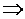 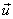 = = 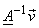 = = 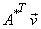
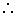 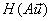 = = 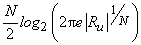 
Use the definition of 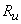 , we have , we have
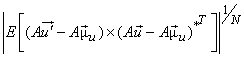 = = 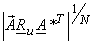 = = 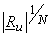
Now
|
= 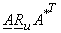 |
| |
= 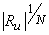 |
Hence
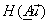 = = 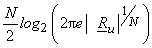 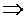 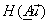 is invariant under any unitary transformation. is invariant under any unitary transformation.
|