Properties of Unitary transforms :(contd.)
2) Energy Compaction Property:
Most unitary transforms have a tendency to pack a large fraction of average energy of an image into relatively few transform coefficients. Since total energy is preserved this implies that many transform coefficients will contain very little energy. If
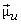 and and 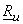 denote the mean and covariance of vector denote the mean and covariance of vector 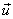 then corresponding quantities for then corresponding quantities for 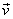 are : are :
And |
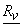 = =
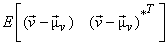 |
| |
= 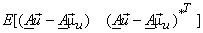 |
| |
= 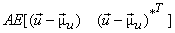 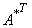 |
| |
= 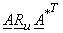 |
Variances of the transform coefficients are given by the diagonal elements of
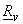 i.e. i.e. 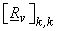 = =
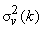
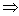 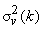 = = 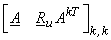
Since 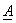 is unitary , it implies: is unitary , it implies:
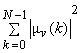 = = 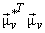 = = 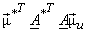 = =
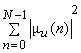
and
|
= 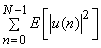 |
|
The average energy 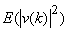 of transform coefficients of transform coefficients 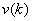 tends to be unevenly distributed, although it may be evenly distributed for input sequence tends to be unevenly distributed, although it may be evenly distributed for input sequence 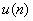 .For a 2D random field .For a 2D random field 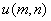 , with mean , with mean 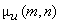 and covariance and covariance 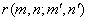 , its transform coefficients , its transform coefficients 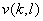 satisfy the properties , satisfy the properties ,
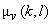 = =
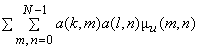
and
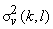 = =
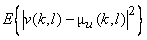 = =
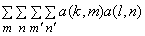 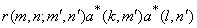
If covariance of 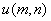 is separable i.e is separable i.e
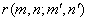 = =
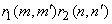
Then variances of transform coefficients can be written as a separable product,
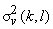 = =
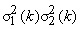
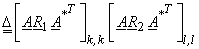
where
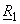 = = 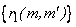 ; ; 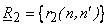
|