Properties of Unitary transforms :
1) Energy conservation :
In the unitary transformation,
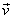 = = 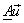 , ,
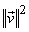 = = 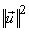
Proof
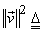 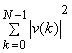 = = 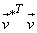 = = 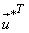 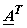 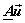 = = 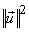 . .
This implies, unitary transformation preserves signal energy or equivalently the length of vector
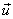 in in
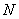 dimensional vector space. That is , every unitary transformation is simply a rotation of dimensional vector space. That is , every unitary transformation is simply a rotation of 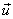 in in
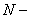 dimensional vector space. Alternatively , a unitary transform is a rotation of basis coordinates and components of dimensional vector space. Alternatively , a unitary transform is a rotation of basis coordinates and components of
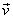 are projections of are projections of 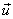 on the new basis. Similarly , for 2D unitary transformations, it can be proved that on the new basis. Similarly , for 2D unitary transformations, it can be proved that
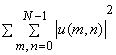 = = 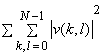
Example: Consider the vector 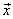 = =  and and 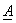 = = 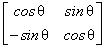
This transformation
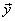 = = 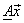 can be written as can be written as 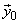 = = 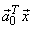 ; ; 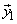 = = 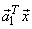 where where
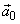 , , 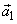 new basis vectors,denote the columns of new basis vectors,denote the columns of 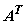 and and 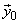 , , 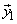 are projections of are projections of 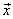 in the new coordinate system. in the new coordinate system.
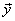 = = 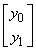 = = 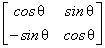  = = 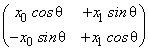
|