Dimensionality of Image transforms
The
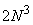 computations for computations for 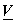 can also be reduced by restricting the choice of can also be reduced by restricting the choice of
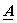 to fast transforms.This implies that to fast transforms.This implies that 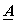 has a structure that allows factorization of the type, has a structure that allows factorization of the type,
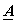 = =
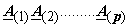
where
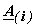 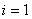 ,...... ,...... 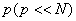 are matrices with just a few non zero entries say are matrices with just a few non zero entries say
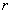 where where
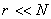 . .
Therefore a multiplication of the type :
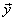 = =
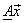 is accomplished in is accomplished in
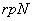 operations.
For several transforms like Fourier, Sine, Cosine, Hadamard etc, operations.
For several transforms like Fourier, Sine, Cosine, Hadamard etc,
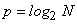 ,
and operations reduce to the order of ,
and operations reduce to the order of
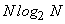 or or
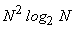 (for (for 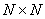 images). images).
Depending on the transform, an operation is defined as 1 multiplication and 1 addition or, 1 addition or subtraction as in Hadamard Transform .
Kronecker products:
If 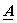 and and 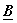 are are 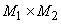 and and 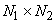 matrices we define Kronecker product as: matrices we define Kronecker product as:
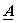  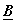  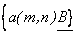
Consider the transform,
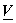 = =
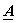 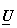 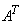
or,
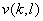 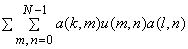
|
(4.1.7) |
If 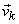 and and 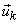 denote denote 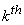 and and 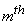 row vectors of row vectors of 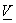 and and 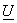 then (7) becomes , then (7) becomes ,
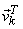 = =
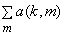 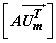 = =
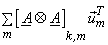 where where 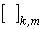 is the is the 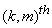 block of block of 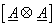
If 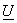 and and 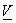 are row ordered into vectors are row ordered into vectors 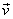 and and 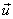 respectively, then respectively, then 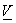 = =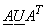  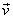 = ( = ( 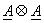 ) ) 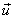 . .
The number of operations required for implementing equation(4.1.7) reduces from 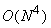 to to 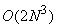 . .
|