Basis Images :
Let 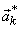 denote denote
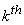 column of column of 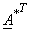 .
Let us define the matrices .
Let us define the matrices
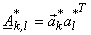 and
matrix inner product of two and
matrix inner product of two
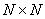 matrices matrices
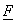 and and
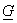 as as
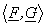 = =

Then equ (4.1.6) and (4.1.5) give a series representation, for the images as ,
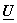 = =
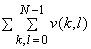 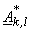 and and
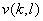 = =
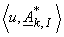
Any image 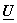 can be expressed as linear combination of can be expressed as linear combination of
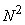 matrices. matrices.
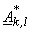 for k,l=0,1,2,.... N-1 are called "basis images". for k,l=0,1,2,.... N-1 are called "basis images".
Therefore any 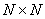 image can be expanded in a series using a complete set of image can be expanded in a series using a complete set of 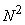 basis images. basis images.
Example: Let 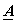 = = 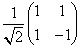 ; ; 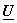 = = 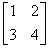
Transformed image 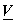 = = 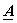 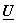 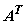 = = 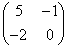 and Basis images are found as outer product of columns of and Basis images are found as outer product of columns of
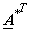 i.e i.e
The inverse transformation 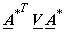 = =
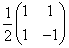 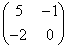  = =  = =
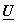
|