Separable Unitary Transforms:
The number of multiplications and additions required to compute transform coefficients
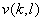 in equation(4.1.3) is in equation(4.1.3) is
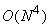 . This is too large for practical size images. If the transform is restricted to be separable, i.e . This is too large for practical size images. If the transform is restricted to be separable, i.e
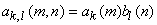  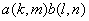
where
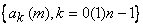 and and
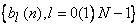 are 1-D complete orthogonal sets of basis vectors. are 1-D complete orthogonal sets of basis vectors.
On imposition of completeness and orthonormality properties we can show that
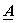  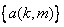 and and
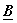  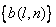 are unitary matrices.i.e are unitary matrices.i.e
Often one chooses
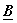 same as same as
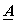 , so that , so that
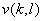 = = 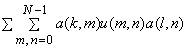 |
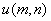 = =
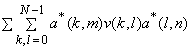
Eqn (4.1.5) can be written as
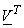 = = 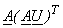 . .
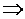 Eqn (4.1.5) can be performed by first transforming each column of Eqn (4.1.5) can be performed by first transforming each column of
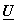 and then transforming each row of the result to obtain rows of and then transforming each row of the result to obtain rows of
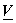 . . |