Two dimensional Orthogonal and Unitary transforms:
As applied to image processing, a general orthogonal series expansion for an 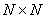 image is a pair of transformations of the form : image is a pair of transformations of the form :
where 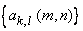 is called an " image transform." is called an " image transform."
It is a set of complete orthogonal discrete basis functions satisfying the properties:-
1) Orthonormality:
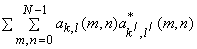 = = 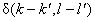
2) Completeness :
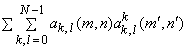 = =
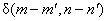
The elements v 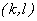 are transform coefficients and are transform coefficients and
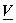  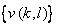 is the transformed image.
The orthonomality property assures that any truncated series expansion of the form is the transformed image.
The orthonomality property assures that any truncated series expansion of the form
| |
for 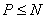 , ,
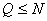 |
|
will minimize the sum of squares error
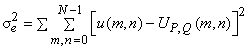 where coefficients where coefficients
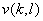 are given by (4.1.3). The completeness property assures that this error will be zero for are given by (4.1.3). The completeness property assures that this error will be zero for 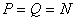 . .
|