Image Transformations
Introduction:
Two dimensional unitary transforms play an important role in image processing. The term image transform refers to a class of unitary matrices used for representation of images. 
In analogy with I-D signals that can be represented by an orthogonal series of basis functions , we can similarly represent an image in terms of a discrete set of basis arrays called " basis images ". These are generated by unitary matrices.
Alternatively an 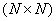 image can be represented as image can be represented as 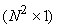 vector. An image transform provides a set of coordinates or basis vectors for the vector space. vector. An image transform provides a set of coordinates or basis vectors for the vector space.
I - D-Transforms:
For a one dimensional sequence 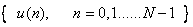 representing a vector representing a vector 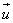 of size N , a unitary transform is : of size N , a unitary transform is : = = 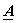 
| |
for 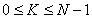 |
(4.1.1) |
where
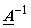 = =
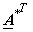 (unitary) (unitary)
This implies ,
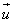 = =
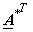 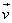
or , 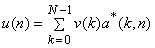 |
for 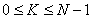 |
(4.1.2) |
Equation (4.1.2) can be viewed as a series representation of sequence u(n) . The columns of
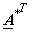 i.e the vectors i.e the vectors
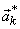 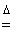 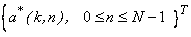 are called the "basis vectors" of are called the "basis vectors" of
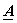 . .
The series coefficients v(k) give a representation of original sequence u(n) and are useful in compression , filtering , feature extraction and other analysis. |