The HAAR Expansion Revisited
Let us split our original set of N input samples  into successive blocks of two, that is, into successive blocks of two, that is,
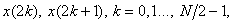 and apply the Haar transform of order and apply the Haar transform of order 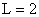 . For each pair of input samples, a pair of transformed samples is obtained, . For each pair of input samples, a pair of transformed samples is obtained,
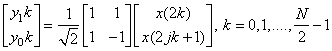
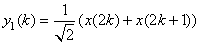 |
(4.7.1) |
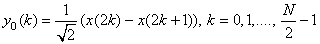 |
(4.7.2) |
This can be interpreted as the action on the sequence of N input samples of two (noncausal) filters with impulse responses and 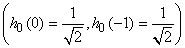 respectively. The corresponding transfer functions are respectively. The corresponding transfer functions are
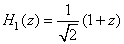 and and
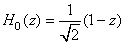

Figure 4.7(a) :Subsampling operation
|
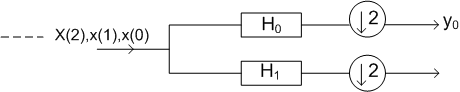
Figure 4.7(b): Filtering interpretation of Haar transformation
|
In other words, the order 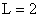 . Haar transform computes the output samples of the two filters when they are fed with the input sequence . Haar transform computes the output samples of the two filters when they are fed with the input sequence
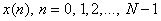 . Furthermore, the output sequence samples are computed for every other sample of the input sequence, at even time instants . Furthermore, the output sequence samples are computed for every other sample of the input sequence, at even time instants 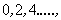 as (4.7.1)and (4.7.2) suggest. This operation is portrayed in Figure (4.7b). The operation at the output of the two filters is known as subsampling by M, in this case as (4.7.1)and (4.7.2) suggest. This operation is portrayed in Figure (4.7b). The operation at the output of the two filters is known as subsampling by M, in this case 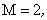 and it is defined in Figure (4.7a). In other words, from the samples
generated at filter output we keep one very and it is defined in Figure (4.7a). In other words, from the samples
generated at filter output we keep one very
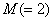 .. In the time domain and for an input sequence consisting of eight samples, the output, .. In the time domain and for an input sequence consisting of eight samples, the output,
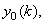 of the of the 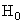 branch of Figure ( ) will consist of four samples given by, branch of Figure ( ) will consist of four samples given by,
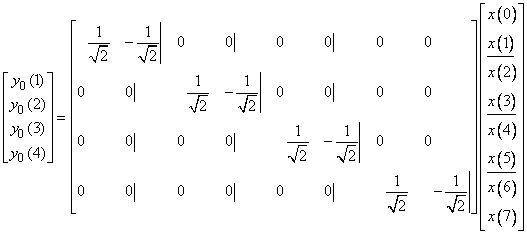
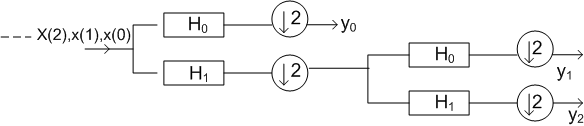
Figure(4.8): Two-stage filtering followed by subsampling operation.
Well, this is nothing other than the action of the last four rows of the 8 x 8 Haar transform in eqn (4.6.3)! What about the rest? Let us carry on the splitting of Figure (4.7b) one step further, as shown in Figure (4.8).
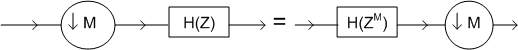
Figure (4.9a):Noble Identity I
|
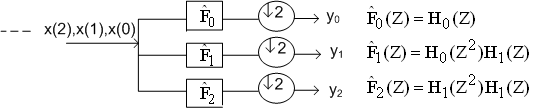
Figure(4.9b):Equivalent Filter Bank of Figure(4.10a)
Using the Noble identity illustrated in Figure (4.9a) the structure of Figure (4.8) turns out to be equivalent to that Figure (4.9b). Taking into account the subsampling operation of the lower branch after the filters 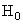 and and 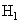 , the Noble identity leads to , the Noble identity leads to
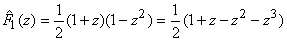
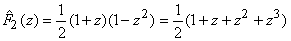
(continued in the next slide) |