The HAAR Expansion Revisited
From the transfer function 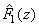 and taking into account the sambsapling by and taking into account the sambsapling by 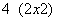 operation, the first two samples of the operation, the first two samples of the 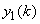 sequence are given by sequence are given by
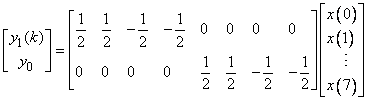
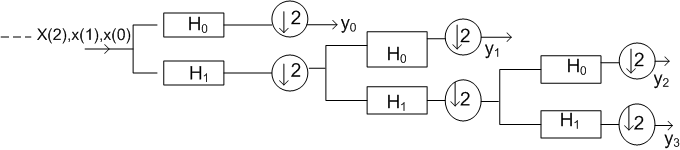
Figure (4.10): Tree-Structure Filter bank
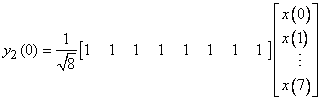
This is nothing but the action of the third and fourth rows of the 8 x 8 Haar tansform on the input vector. If we now carry on the splitting one step further, as in Figure (4.10), it is straightforward to show by repeating the preceding arguments that
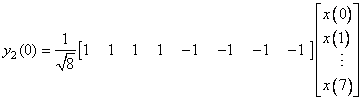
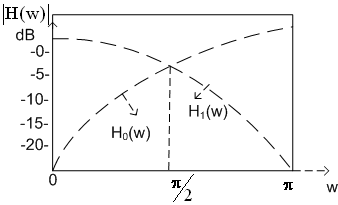
Figure(4.11) Magnitude response of the Haar filters H0 and H1
These equations are the actions of the second and first rows of the Haar tansform on the input vector. The structure of Figure (4.10) is known as a (three-level) tree-structured filter bank generated by the filters
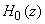 and and
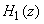 . Figure (4.11) shows the frequency responses of these two filters. One . Figure (4.11) shows the frequency responses of these two filters. One
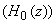 is a high-pass filter and the other a low-pass filter. Here in lies the importance of the filter band interpretation of the Haar transform. The input sequence is a high-pass filter and the other a low-pass filter. Here in lies the importance of the filter band interpretation of the Haar transform. The input sequence
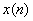 is first split into two versions of lower resolution with respect to the original one: a low-pass (average) coarser resolution version and a high-pass (difference) detailed resolution one. In the sequel the coarser resolution version is further split into two versions, and so on. This leads to a number of versions with a hierarchy of resolutions. This decomposition is known as multiresolution decomposition . is first split into two versions of lower resolution with respect to the original one: a low-pass (average) coarser resolution version and a high-pass (difference) detailed resolution one. In the sequel the coarser resolution version is further split into two versions, and so on. This leads to a number of versions with a hierarchy of resolutions. This decomposition is known as multiresolution decomposition . |