Table (4.5.1 ): Parameters for the Haar functions
K |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
P |
0 |
0 |
1 |
2 |
2 |
2 |
2 |
2 |
q |
0 |
1 |
1 |
1 |
1 |
1 |
3 |
4 |
The Haar transform matrix of order L consists of rows resulting from the preceding functions computed at the points 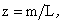 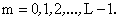 For example, the 8 x 8 transform matrix is
 |
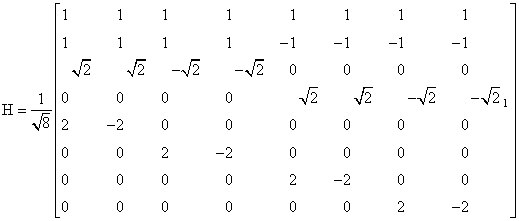(4.6.3) |
It is not difficult to see that 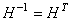 that is H is orthogonal.
The energy packing properties of the Haar transform are not very good. However, its importance for us lies beyond that. We will use it as the vehicle to take us from the world of unitary transforms to that of multiresolution analysis. To this end, let us look carefully at the Haar transform matrix. We readily observe its sparse nature with a number of zeros, whose location reveals an underlying cyclic shift mechanism. To satisfy our curiosity as to why this happens, let us look at the haar transform from a different perspective |
which are defined in the closed interval 
.The order k of the function is uniquely decomposed into two integers p,q 
for 
and 
or 1 for 
The Haar functions are 
