Karhunen-Loeve Transform (KLT ) (continued)
To show that of all possible linear transforms operating on length N vectors having stationary statistics, the KTL minimizes the MSE due to truncation.
Let 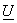 be some other transform having unit length basis vectors be some other transform having unit length basis vectors 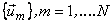
First we show heuristically that the truncation error is minimum if the basis vectors  are orthogonalised using the well known Gram Schmidt procedure. are orthogonalised using the well known Gram Schmidt procedure.
Let 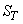 be the vector space spanned by the "transmitted" vectors: be the vector space spanned by the "transmitted" vectors:  for for 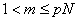 and let and let
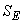 be the space spanned by the remaining vectors. Therefore any vector be the space spanned by the remaining vectors. Therefore any vector 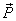 can be represented by can be represented by 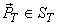 plus vector plus vector 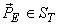 i.e, as shown in figure below. i.e, as shown in figure below.
If 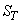 is the space spanned by transmitted basis vector, then truncation error is the length of vector is the space spanned by transmitted basis vector, then truncation error is the length of vector 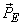 . Error is minimized if . Error is minimized if 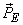 is is  to to 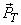 . .
If only 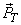 is transmitted, then MSE is the squared length of the error vector is transmitted, then MSE is the squared length of the error vector 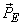 , which is clearly minimized if , which is clearly minimized if 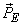 is orthogonal to is orthogonal to 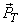 i.e., i.e., 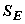 is orthogonal to is orthogonal to 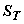 . Further orthogonalisation of the basis vectors within . Further orthogonalisation of the basis vectors within 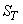 , or within , or within
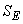 , does not affect MSE. , does not affect MSE.
Thus we assume 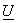 to be unitary i.e., to be unitary i.e., 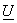 has orthogonal basis vectors i.e. has orthogonal basis vectors i.e.
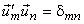
Its transform coefficients are then given by
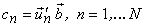
The mean square truncation error is as given by eqn ( ) is,
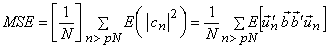 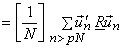
Now suppose we represent the vectors  in terms of KTL basis vectors in terms of KTL basis vectors 
i.e., 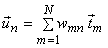
and, 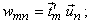 This follows from This follows from 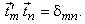
Since 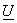 is unitary is unitary
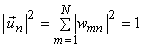 (because basis vectors are of unit length) (because basis vectors are of unit length)
Now from equation ( ) we have
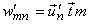 |
() |
and therefore  can be written in terms of can be written in terms of  as, as, 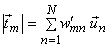 (continued in the next slide) |