Karhunen-Loeve Transform (KLT ) (continued)
From the normality or unitary transform condition i.e., 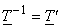 we get we get 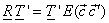 with the variances of with the variances of 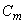 along the main diagonal of the matrix. Thus, in terms of column vectors of along the main diagonal of the matrix. Thus, in terms of column vectors of 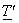 , the above equation becomes , the above equation becomes
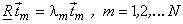
We see that the basis vectors of the KLT are the eigenvectors of 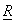 , orthonormalised to satisfy , orthonormalised to satisfy 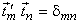
[Note that whereas the other image transforms like DFT, DCT were independent of data, the KLT transformation depends on 2nd order satisfies of the data.]
The variances 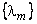 of the KLT coefficients are the eigenvalues of of the KLT coefficients are the eigenvalues of 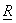 and since and since 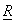 is symmetric and positive definite, eigenvalues are real and positive. The KLT basic vectors and transform coefficients are also real. Besides decorrelating transform coefficients, the KLT has another useful property: it maximizes the number of transform coefficients that are small enough so that they are insignificant. For example, suppose the KLT coefficients is symmetric and positive definite, eigenvalues are real and positive. The KLT basic vectors and transform coefficients are also real. Besides decorrelating transform coefficients, the KLT has another useful property: it maximizes the number of transform coefficients that are small enough so that they are insignificant. For example, suppose the KLT coefficients
 are ordered according to decreasing variance ie are ordered according to decreasing variance ie 
Also suppose that for reasons of economy, we transmit only the 1st pN coefficients where 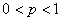 . The receiver then uses the truncated column vector . The receiver then uses the truncated column vector 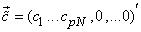 to form the reconstructed values as to form the reconstructed values as 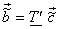 . .
The mean squared error (MSE) between the original 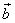 and the reconstructed pels and the reconstructed pels 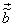 is then is then
It can be shown that KLT minimizes the MSE due to truncation.
(continued in the next slide) |