Karhunen-Loeve Transform (KLT )
So far no transformation has been found for images that completely removes statistical dependence between transformation coefficients. Suppose a reversible transformation is carried out on N-dimensional vector 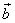 to produce N-dimensional vector to produce N-dimensional vector 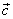 of transform coefficients, denoted by, of transform coefficients, denoted by,
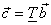 |
(4.4.1) |
where 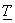 is a linear transformation matrix that is orthonormal or unitary; is a linear transformation matrix that is orthonormal or unitary;
| ie |
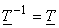 |
(4.4.2) |
(where "1" denotes transpose)
Denote the m th column of matrix 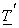 by column vector by column vector 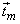 , then eqn (4.4.2 ) is equivalent to , then eqn (4.4.2 ) is equivalent to 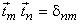
The vectors 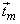 are called orthonormal basis vectors for linear transform are called orthonormal basis vectors for linear transform 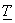 . .
From eqn (4.4.1) we can express 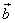 as, as,
where 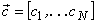 are transform coefficients, and are transform coefficients, and 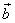 is represented as a weighted sum of basis vectors. is represented as a weighted sum of basis vectors.
KLT transform is an orthogonal linear transformation that can remove pairwise statistical correlation between the transform coefficients; ie the KLT transform coefficients satisfy 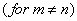
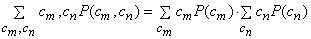
where summation is over all possible values 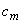 and and 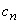 and P( ) represents the probability. and P( ) represents the probability.
This is usually written using the statistical averaging operator E as,
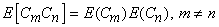 or or
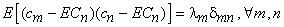
where 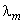 is the variance of is the variance of 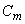 . .
Note that statistical independence implies uncorrelation, but the reverse is not generally true (except for jointly Gaussian r v s )
The KLT can be derived by assuming
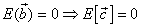
The N x N correlation matrix of 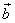 then becomes then becomes
(continued in the next slide) |