Symmetric Extension in 2-D DCT
Since the 2-D DCT 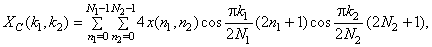
is just the separable operator resulting from application of the 1-D DCT along first one dimension and then the other, the order being immaterial, we can easily extend the 1-D DCT properties to the 2-D case. In terms of the connection of the 2-D DCT with the 2-DFT, we thus see that we must symmetrically extend in, say, the horizontal direction and then symmetrically extend that result in the vertical direction. The resulting symmetric function (extension) becomes
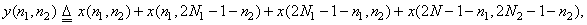
The symmetry is about the lines 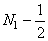 and and 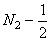 then from (4.3.7), it follows that the 2-D DCT is given in terms of the then from (4.3.7), it follows that the 2-D DCT is given in terms of the
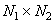 point DFT as point DFT as
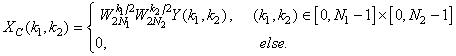
Comments
• We see that both the 1-D and 2-D DCTs involve only real arithmetic for real-valued data, and this may be important in some applications.
• The symmetric extension property can be expected to result in fewer high frequency coefficients in DCT with respect to DFT. Such would be expected for lowpass data, since there would often be a jump at the four edges of the 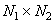 period of the corresponding periodic sequence period of the corresponding periodic sequence 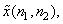 which is not consistent with small high- frequency coefficients in the DFS or DFT. Thus the DCT is attractive for lossy data storage applications, where the exact value of the data is not of paramount importance. which is not consistent with small high- frequency coefficients in the DFS or DFT. Thus the DCT is attractive for lossy data storage applications, where the exact value of the data is not of paramount importance.
• The DCT can be used for a symmetrical type of filtering with a symmetrical filter.
• 2-D DCT properties are easy generalizations of 1-D DCT properties. |