Some 1-D DCT Properties (contd.)
It turns out that eigenvectors of the unitary DCT are the same as those of the symmetric tridiagonal matrix,

and this holds true for arbitrary values of the parameter 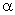 . We can relate this matrix Q to the inverse covariance matrix of a 1-D first-order stationary Markov random sequence, with correlation coefficient . We can relate this matrix Q to the inverse covariance matrix of a 1-D first-order stationary Markov random sequence, with correlation coefficient 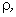 necessarily satisfying necessarily satisfying 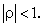
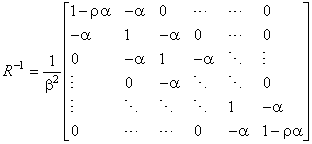
where 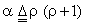 and and 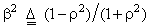 . The actual covariance matrix of the Markov random sequence is . The actual covariance matrix of the Markov random sequence is

with corresponding, first-order difference equation,

It can further be shown that when 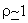 , ,
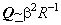 , so that eigenvectors approximate each other too. Because the eigenvectors of a matrix and its inverse are the same, we then have the fact that the unitary DCT basis vectors approximate the Karhunen-Loeve expansion, with basis vectors given as the solution to the matrix-vector equation, , so that eigenvectors approximate each other too. Because the eigenvectors of a matrix and its inverse are the same, we then have the fact that the unitary DCT basis vectors approximate the Karhunen-Loeve expansion, with basis vectors given as the solution to the matrix-vector equation,
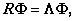
And corresponding Karhunen-Loeve transform (KLT) given by
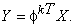
Thus the 1-D DCT of a first-order Markov random vector of dimension N should be close to the KLT of x when its correlation coefficient 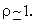 This ends the review of the 1-D DCT. This ends the review of the 1-D DCT. |