Some 1-D DCT Properties
1) Linearity:
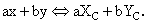
2) Energy conservations:
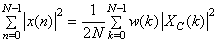 |
(4.3.8) |
3) Symmetry:
(a) General case:

(b) Real-valued case:
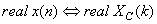
4) Eigenvectors of unitary DCT: Define the column vector
 and define the matrix C with elements: and define the matrix C with elements:
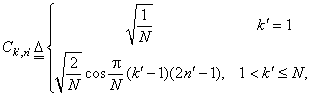
Then the vector 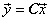 contains the unitary DCT, whose elements are given as contains the unitary DCT, whose elements are given as 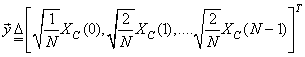
A unitary matrix is one whose inverse is the same as the transpose 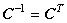 . For the unitary DCT, we have . For the unitary DCT, we have
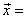 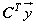
and energy balance equation,

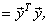
which is a slight modification on the DCT Parseval relation (4.3.8). So the unitary DCT preserves the energy of the signal x. (continued in the next slide)
|