Review of 1- D DCT
In the 1-D case the DCT is defined as
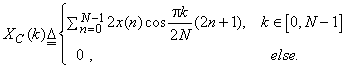 |
(4.3.4) |
for every N point signal 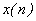 having support having support 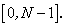 The corresponding inverse transform, or IDCT, can be written as The corresponding inverse transform, or IDCT, can be written as
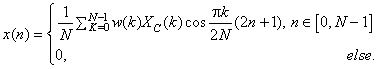 |
(4.3.5) |
It turns out that this 1-D DCT can be understood in terms of the DFT of a symmetrically extended sequence,
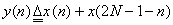 |
(4.3.6) |
This is not the only way to symmetrically extend x , but this method results in the most widely used DCT sometimes called DCT-2 with support 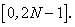 In fact, on defining the 2N point DFT In fact, on defining the 2N point DFT 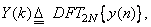 we will show that the DCT can be alternatively expressed as we will show that the DCT can be alternatively expressed as
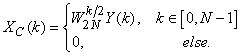 |
(4.3.7) |
Thus the DCT is just the DFT analysis of the symmetrically extended signal defined in (4.3.6):
Looking at this equation, we see that there is no overlap in its two components, which fit together without a gap. We can see that right after 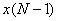 comes comes 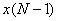 at position at position 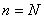 , which is then followed by the rest of the nonzero part of x in reverse order, upto , which is then followed by the rest of the nonzero part of x in reverse order, upto 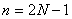 , where sits , where sits
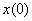 .We can see a point of symmetry midway between .We can see a point of symmetry midway between 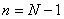 and N, i.e., at and N, i.e., at 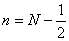 . .
If we consider its periodic extension 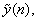 we will also see a symmetry about the point we will also see a symmetry about the point 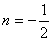 . We thus expect that the 2N point . We thus expect that the 2N point 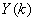 will be real valued except for the phase factor will be real valued except for the phase factor 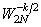 . So the phase factor in eqn (4.3.7) is just what is needed to cancel out the phase term in Y and make the DCT real , as it must if the two equations, (4.3.1) and (4.3.7), are to agree for real valued inputs x. . So the phase factor in eqn (4.3.7) is just what is needed to cancel out the phase term in Y and make the DCT real , as it must if the two equations, (4.3.1) and (4.3.7), are to agree for real valued inputs x.
To reconcile these two definitions, we start out with eqn (4.3.7), and proceed as follows:
the last line following from 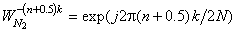 and Euler's relation, which agrees with the original definition, eqn (4.3.4). and Euler's relation, which agrees with the original definition, eqn (4.3.4).
The formula for the inverse DCT, can be established similarly, starting out from
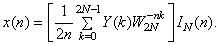 |