Karhunen-Loeve Transform (KLT ) (continued)

Since the KTL is unitary,

We may now write

which form eqn ,	we get

As 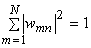,	we have

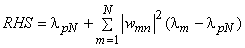ie

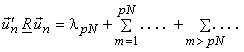which is

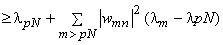(Since for )

Thus from eqn for

we have

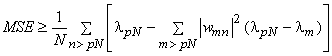The second summation	ie

and since

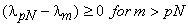we have

ie	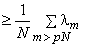which is = MSE for KTL

This concludes that the MSE for any other linear transform exceeds that of the KTL transform.