(contd. )
In the Fourier integrals of (1) and (2), the coordinate positions in the signal and frequency domains can now be expressed by the respective mapping functions such that,
and
The signal amplitudes shall not be changed by the coordinate mapping i.e.
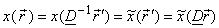 |
(3.2.8) |
The spectral values must also uniquely be mapped, but may be subject to a constant scaling of amplitudes,
Then, comparing eqn(3.2.4) ,(3.2.5) to (3.2.9) we get.
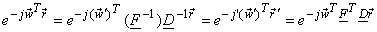
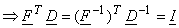
and as
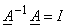
we have,
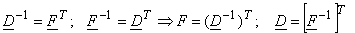
For the 2D case 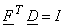 imposes four conditions on the basis vectors: imposes four conditions on the basis vectors:
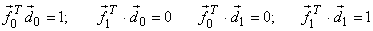 ; ;
It is evident that each basis vectors 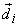 in spatial domain has its orthogonal counterpart in spatial domain has its orthogonal counterpart 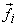 in frequency domain s.t. in frequency domain s.t. 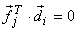 for for 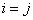 ;. ;.
For 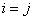 ; the inner product of vectors is unity. We say that the basis systems described by ; the inner product of vectors is unity. We say that the basis systems described by 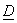 and and 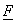 are bi-orthogonal are bi-orthogonal 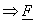 is the dual matrix of is the dual matrix of 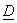 . .
(continued in the next slide) |