Coordinate Systems Mapping
Rectangular coordinate systems are only a special case for the description of two dimensional signals. They allow expressing the relationships between spatial domain and frequency domain by a 2D FT with separable integration over the different dimensions.
Example: The 2D FT of a spatially continuous signal 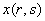 is defined as, is defined as,
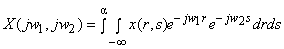
Alternatively provided that the coordinated axes establish an orthogonal system, this equation can be represented as,
where 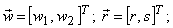 The rectangular 2D coordinate system is described by a reference system of unit vectors
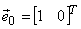 and and 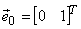 which establish orientations of orthogonal axes. which establish orientations of orthogonal axes.
Any coordinated pair (r, s) can then be expressed as a vector 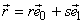 .The relationship with frequency vectors .The relationship with frequency vectors  is given by equ(1), where the coordinate system describing the frequency plane must be based on orthogonal axes of same orientations as shown below. is given by equ(1), where the coordinate system describing the frequency plane must be based on orthogonal axes of same orientations as shown below.
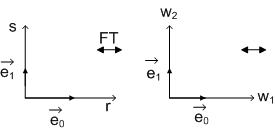
Figure(3.2.13) We apply a coordinate mapping 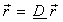 where mapping matrix D is, where mapping matrix D is,
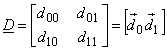
The vectors 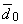 and and 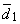 are referred to as basis vectors of the mapping. A complementary mapping in the frequency plane is given by are referred to as basis vectors of the mapping. A complementary mapping in the frequency plane is given by 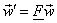 where where
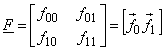
Unless the determinants 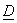 or or 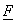 are zero, the mappings must be reversible such that are zero, the mappings must be reversible such that
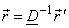
and
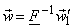
The FT in the mapped coordinate system can then be expressed as:
(continued in the next slide) |