Some examples
1) Scaled rectangular mapping
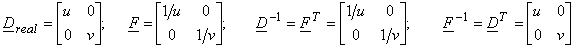
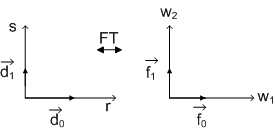
Figure(3.2.14) 2) Shear mapping
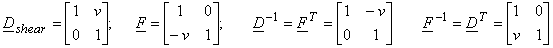
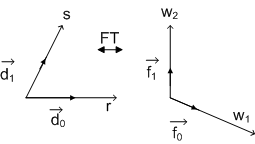
Figure(3.2.15)
3) Quincunx mapping
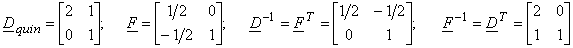
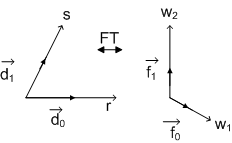
Figure(3.2.16)
4) Hexagonal mapping
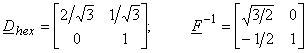
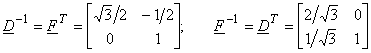
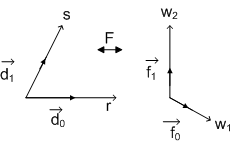
Figure(3.2.17)
5) Rotational mapping: Clockwise by angle 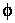
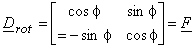
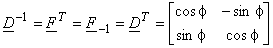
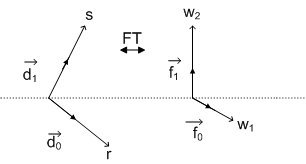
Figure(3.2.18)
Note The scaled rectangular transformation describes the scaling property of Fourier transform, where the amplitude factor results from the determinant of transformation matrix i.e.,
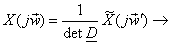 obtained using obtained using 
i.e.
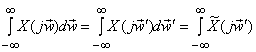
The shear mapping in principle allows redefining the angular orientation of 2D signals while horizontal spectral characteristics are retained (in the case where only the vertical axis is sheared). Coordinate transformations introduced here allow understanding of the impact of geometric modifications on the spectra of 2D signals. These relationships can be also be used to analyze sampling of 2D signals. |