Spectrum of the Sampled Signal:
We now relate the Fourier transform
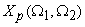 or or 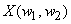 of the sampled signal to that of the continuous signal of the sampled signal to that of the continuous signal
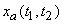 . .
As given earlier, the 2D continuous space Fourier transform
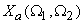 of a signal of a signal
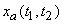 with continuous variables with continuous variables
 is given by, is given by,
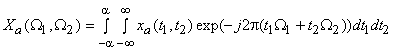 |
(3.1.4) |
where
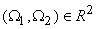 and the inverse Fourier transform is given by, and the inverse Fourier transform is given by,
Here the spatial frequency variables
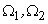 have the units in cycles/mm and are related to radian frequencies by a scale factor of have the units in cycles/mm and are related to radian frequencies by a scale factor of 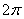 . .
In order to evaluate the 2D FT
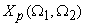 of of
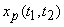 we substitute equ (3.1.3) in to equ (3.1.4) and exchange the order of we substitute equ (3.1.3) in to equ (3.1.4) and exchange the order of
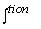 and summation to obtain, and summation to obtain,
which simplifies as,
(continued)
|