Spectrum of the Sampled Signal: (contd:)
Note that
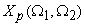 is periodic with the fundamental period given by the region, is periodic with the fundamental period given by the region,
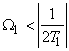 and and
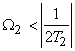
Letting
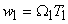 and and
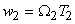 and using equ (3.1.2), we obtain the discrete space Fourier transform relation, in terms of unitless frequency variables and using equ (3.1.2), we obtain the discrete space Fourier transform relation, in terms of unitless frequency variables
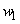 and and 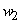 as, as,
The 2D discrete-space inverse Fourier Transform is given by
Note that the discrete-space Fourier transform
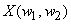 is periodic with the fundamental period is periodic with the fundamental period
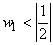 and and
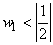 . .
The standard approach to relate FT
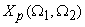 or or
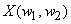 of the sampled signal to the continuous is to start with equ (3.1.3) and express of the sampled signal to the continuous is to start with equ (3.1.3) and express
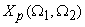 as the 2D convolution of Fourier transforms of the continuous signal and the 2D impulse train (also called comb function) using the modulation property of the FT: as the 2D convolution of Fourier transforms of the continuous signal and the 2D impulse train (also called comb function) using the modulation property of the FT:
where FT denotes 2D FT.
The FT
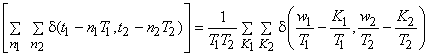
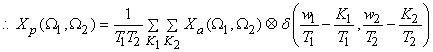
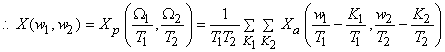
|