Introduction
It is generally true that all discrete sequences are formed in an attempt to represent some underlying continuous signal. Although many discrete representations of continuous signals are possible, periodic sampling is by far the representation mostly used due to the simplicity of its implementation. We consider, in this section, the relationships between continuous signals and the discrete sequences which are obtained from them by periodic sampling. In particular, we first consider the specific case of rectangular periodic sampling, and then a more general case of periodic sampling with arbitrary sampling geometries.
Two Dimensional Rectangular Sampling :
We discuss 2D rectangular sampling of a stillerriage
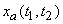 in two spatial coordinates. In spatial rectangle sampling, we sample at the locations.
in two spatial coordinates. In spatial rectangle sampling, we sample at the locations.
where 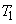 and
and
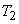 are sampling distances in the
are sampling distances in the 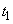 and
and 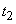 directions, respectively.
directions, respectively.
The 2D rectangular sampling grid is depicted in figure below.
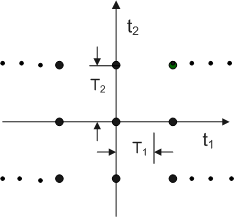
Figure(3.1.1)
The sampled signal can be expressed in terms of the unitless coordinate variables
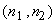 as:
as:
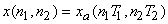 for all for all
|
|
|
In some cases it is convenient to define an intermediate sampled signal in terms of continuous coordinate variables given by,
Note 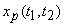 is indeed a sampled signal because of the presence of 2D Dirac delta functions.
is indeed a sampled signal because of the presence of 2D Dirac delta functions.