2.3.2 MVU Estimator and CRLB Attainment
In general, an MVU estimator may exist but may not attain the CRLB. To illustrate this, let us assume that there exist three unbiased estimators for estimating the unknown parameter θ in an estimation problem and their variances are shown in Figure 2.3
. As shown in Figure 2.3
(a), the estimator 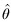 3 is the efficient as it attains the CRLB and therefore it is also MVUE. On the other hand, in Figure 2.3
(b), the estimator
3 is the efficient as it attains the CRLB and therefore it is also MVUE. On the other hand, in Figure 2.3
(b), the estimator 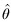 3 does not attain the CRLB so it is not an efficient. But its variance is uniformally less that other possible unbiased estimators so it is the MVUE.
3 does not attain the CRLB so it is not an efficient. But its variance is uniformally less that other possible unbiased estimators so it is the MVUE.
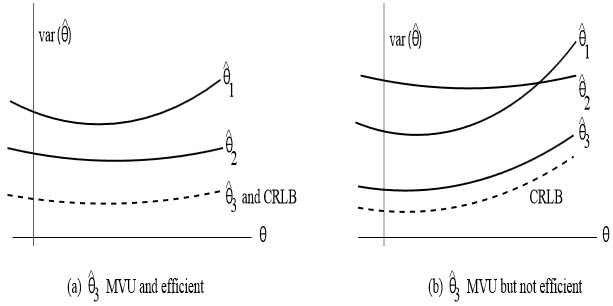
Figure 2.3: Possible dependence of estimator variance with parameter θ
2.3.3 Fisher Information
As noted above, when CRLB is attained, the variance of the unbiased estimator is reciprocal of the Fisher information. The Fisher information is a way of measuring the amount of information that an observable random variable x carries about an unknown parameters θ upon which the probability of x depends. Assume that the data PDF p(x; θ) satisfies some regulairty conditions which include:
- For all x such that p(x; θ) > 0,
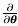 ln p(x; θ) exists and is finite.
ln p(x; θ) exists and is finite. - The operation of the integration with respect to x and the differentiation with respect to θ could be exchanged in finding the expectation, i.e.,
![]()
Note that the above regularity conditions are satisfied in general except when the domain of the PDF for which it is nonzero dependes on the unknown parameter (e.g., uniform distribution 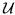 (0,θ) with unknown domain parameter).
(0,θ) with unknown domain parameter).
Given the PDF p(x; θ), the Fisher information I(θ) can also be expressed as
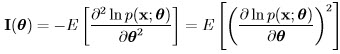
which follows directly from the “regularity” condition, E![[ ] ∂lnp(x;θ) ∂θ](images/14.jpg) = 0 ∀ θ , imposed on the PDF.
= 0 ∀ θ , imposed on the PDF.
Proof
2.3.4 Example
2.3.5 Consistency of Estimator
Another desirable property of estimators is consistency. If we collect a large number of observations, we hope that we have a lot of information about any unknown parameter θ, and thus we can construct an estimator with a very small mean square error (MSE). An estimator is defined as consistent if
![]()
which means that as the number of observations increase the MSE of the estimator descends to zero, i.e., 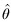 = θ.
= θ.
For an example, if  , then the MSE of
, then the MSE of 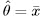 is 1∕n. Since limn (1∕n) = 0, x is a consistent estimator of θ or more specifically “MSE-consistant”. There are other type of consistancy definitions that look at the probability of the errors. They work better when the estimator do not have a variance.
is 1∕n. Since limn (1∕n) = 0, x is a consistent estimator of θ or more specifically “MSE-consistant”. There are other type of consistancy definitions that look at the probability of the errors. They work better when the estimator do not have a variance.
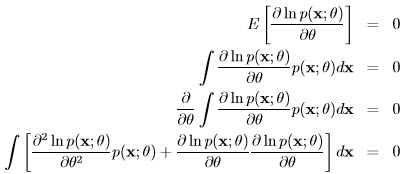
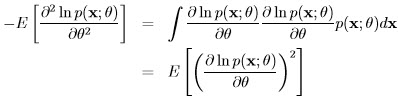
![[( ) ] ∂lnp(x;θ)-2 ∂θ](images/17.jpg)
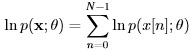
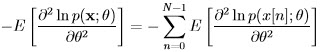
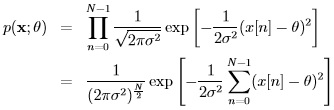
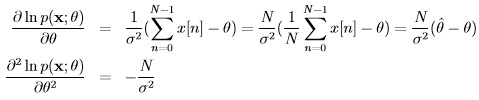
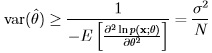
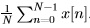 . Shown earlier that for estimation of DC level in WGN, the sample-mean estimator has a variance of
. Shown earlier that for estimation of DC level in WGN, the sample-mean estimator has a variance of 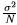 . Thus it is indeed an MVUE as its variance achieves the minimum possible variance bound of
. Thus it is indeed an MVUE as its variance achieves the minimum possible variance bound of 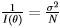 .
.