In this lecture, we present the Cramer Rao lower bound on the variance of an unbiased estimator.
2.3.1 Cramer Rao Lower Bound (CRLB)
The variance of any unbiased estimator 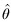 under certain regularity conditions, must be lower bounded by the CRLB, with the variance of the MVUE attaining the CRLB. That is:
under certain regularity conditions, must be lower bounded by the CRLB, with the variance of the MVUE attaining the CRLB. That is:
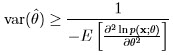
and
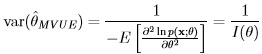
where I(θ) = ![[ ] ∂2lnp(x;θ) ∂θ2](images/3.jpg) is the Fisher information.
is the Fisher information.
Furthermore if, for some function g amd I:
![]()
then we can find the MVUE as: 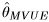 = g(x) and the minimum, variance is
= g(x) and the minimum, variance is 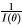 . The proof of these results are given later in Section 2.4.1
. The proof of these results are given later in Section 2.4.1
For p-dimensional parameter, θ, the equivalent condition in terms of the covariance matrix is given by:
![]()
i.e., C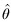 - I-1(θ) is positive semi-definite where C
- I-1(θ) is positive semi-definite where C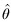 = E[(
= E[(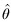 -E(
-E(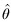 ))((
))((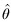 -E(
-E(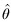 ))T ] is the covariance matrix of the estimator. The Fisher matrix, I(θ), is given as:
))T ] is the covariance matrix of the estimator. The Fisher matrix, I(θ), is given as:
![]()
Furthermore if, for some p-dimensional function g and p × p matrix I:
![]()
then we can find the MVUE as: 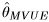 = g(x) and the minimum covariance is I-1(θ).
= g(x) and the minimum covariance is I-1(θ).