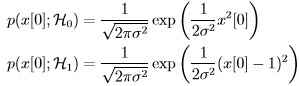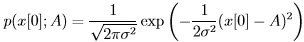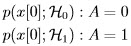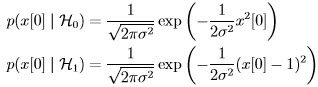Classification of Estimation Approaches
Based on the assumptions made about the unknown parameter, the estimation methods can be classified into two broad groups: classical parameter estimation and Bayesian estimation. In the classical parameter estimation methods, no probabilistic assumption about the unknown parameter is made; rather it is treated as the deterministic unknown. In both these broad groups, a number of optimal and suboptimal estimation approaches exist which are necessitated by the lack of the complete knowledge about the mathematical model available for estimating the unknown quantity. A broad classification of different estimation methods are given Table 1.1.
| Unknown param. | Probabilistic assumption | Other requirement | Estimator kind (salient property) | Practical utility |
|---|---|---|---|---|
Non-random |
Completely known PDF |
Sufficeient statistics | Minimum variance unbiased (optimal) | Low |
| Large data; no statistics | Maximum likelihood (asymptotically optimal) | Very high | ||
| First-two moments only | Best linear unbiased (suboptimal in general) | Moderate | ||
| Known signal model; no PDF | Least squares (suboptimal) | High | ||
Random |
Known joint and prior PDFs |
Conjugate prior; quadratic cost | Minimum mean square error (optimal) | High |
| Hit-or-Miss cost | Maximum a posteriori | High | ||
| Uniform prior; Hit-or-Miss cost | Bayesian maximum likelihood | Low | ||
| First-two moments only | Linear minimum mean square error; Wiener filter (suboptimal in general) | Very high |
Table 1.1: Classification of different estimation approaches.
1.1.2 Formulation of the Detection Problem
The simplest detection problem is formed when we wish to decide whether a signal is present embedded in noise or if only noise is present. For example, consider the detection of an aircraft based on radar echo. This problem can be termed as binary hypothesis testing problem, the two hypothesis being (1) the aircraft is absent, (2) the aircraft is present. A somewhat more general binary hypothesis testing problem is encountered in communications. There our interest is in deciding which of two possible signals is transmitted. For example our hypothesis in this case consists of a sinusoid of phase 0° embedded in noise verse a sinusoid with phase 180° embedded in noise. Frequently, we also wish to decide among more than two hypotheses. For example in speech recognition, our goal is to determine which of the digit among ten possible ones is spoken. Such problem is referred to as multiple hypothesis testing problem.
All these problems are characterized by the need to decide among two or more possible hypotheses based on the observed data set. As always, the data are inherently random in nature due to the inherent variability and noise, so that a statistical approach is necessitated. We model the detection problem in a form that allows us to apply the theory of statistical hypothesis testing.
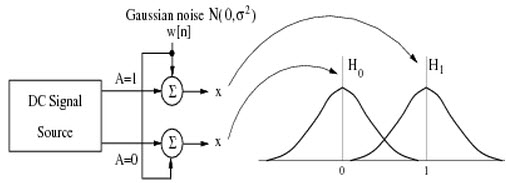
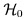, which is noise-only hypothesis, and 
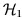, which is the signal-present hypothesis, or symbolically:
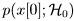and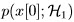 
, which for this example are:
