Eqn.(11) is the same as eqn.(6), if electric field E seen by the orbiting electron is the Coulomb field 
without the Thomas factor and the relativistic factor 
. Therefore for a non-relativistic electron, the magnetic field appearing at the orbiting electron can be derived from Biot-Savart's law without invoking Lorentz transformation. Now, the eqn.(11) can be written as
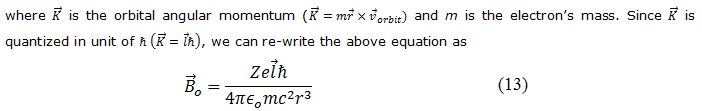
Substituting the eqn.(13) in eqn.(8), we get
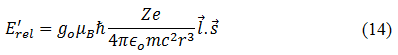
After adding the Thomas correction, eqn.(14) becomes
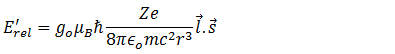
The above energy depends on the scalar product 
, where 
is the orbital quantum number and 
is the spin quantum number. Hence, the above equation represents spin-orbit interaction. Since Dirac has shown that g0 = 2 for a free electron, the spin-orbit Hamiltonian will be
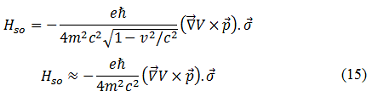
where the electric field is related to the electric potential V as 
and the velocity operator is 
where 
is the momentum operator.