The negatively charged electron in an atom orbiting around the nucleus (see Figure 4.1) feels the electric field due to the positively charged nucleus. As a result, a magnetic field will appear in the rest frame of the electron as follows: If we sit on the electron, the proton will appear to rotate around us and create a circular loop of current I as given by,

..........

where, v is velocity of proton moving on circular orbit, T is the period of rotation, and R is the radius of the circular orbit. According to Biot-Savart's law, the magnetic flux density at a distance x along the line passing through the center of the proton orbit and perpendicular to the plane of the orbit is given by,

........

So, in the plane of the orbit, where x = 0, the eqn.(2) turns out to be

In addition, it is known that c²=1/(μ₀ε₀), where μ₀ is permeability of free space and ε₀ is permittivity of free space, Hence, we get,

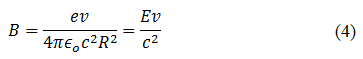
Eqn.(4) can be written in a vectorial form in the rest frame of the electron as

.........

where, the factor ½ is the Thomas correction factor [1]. The electron in a rotating orbit is constantly accelerating because the direction of the velocity is changing with time, even though the magnitude is not changing. Therefore, it is not enough to transform the laboratory frame to the rest frame using the electron's instantaneous velocity. On the other hand, an observer in the electron's rest frame finds that an additional rotation is required to align the observer's coordinate axes with the ones obtained by Lorentz transforming the laboratory frame. Hence, the additional factor 2 is needed to be introduced when the above fact is taken into account [1].