............
...

In addition, Pauli also defined the first three dimensionless matrices σ_x, σ_y, and σ_z such that

Since, S_x, S_y, and S_z must have Eigenvalues of ± ћ/2, the σ matrices have Eigenvalues of ±1. Furthermore, eqn.(8) mandates that

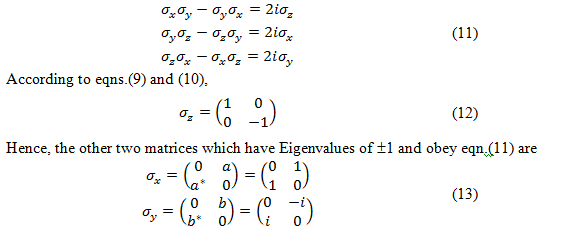
where a = 1, a* = 1, b = -i, and b* = +i. These are called Pauli spin matrices and serve as operators for the spin components according to eqn.(10).

Note that the square of each of the Pauli matrices is the 2×2 unit matrix [I]. Hence,

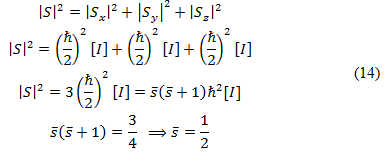
Eigenvectors of the Pauli matrices: SPINORS

In quantum mechanics, the state of any physical system is identified with a ray (in a complex separable Hilbert space) or by a point (projective Hilbert space). Each vector in the ray is called 'ket' expressed symbolically as |ψ >.