Pauli Spin Matrices:

The inclusion of spin part was investigated by Wolfgang Pauli, who derived an equation to replace eqn.(5) which is known as the Pauli equation. In quantum mechanics, any physical observable is associated with an operator (linear in case of Schrödinger formalism and matrix in Heisenberg formalism). The Eigenvalues of the linear operator are the expectation values of the physical quantity, i.e., the values we expect to find if we measure the physical quantity in an experiment. Spin is a physical observable, since the associated angular momentum can be measured (discussed in Stern-Gerlach experiment). Thus, there must be a quantum mechanical operator associated with the spin. Pauli derived the quantum mechanical operators for the spin components along with three orthogonal axes S_x, S_y, S_z which are 2×2 matrices known as Pauli spin matrices. Pauli approach was based on (i) the measurement of spin angular momentum component along any coordinate axes for an electron should give result as +ћ/2 or –ћ/2, (ii) the operations for spin components along three mutually orthogonal axes should obey commutation rules similar to those obeyed by the operators associated with the components of orbital angular momentum.

The operators for the orbital angular momentum are known to satisfy the commutation relations,

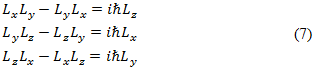
Where L_x, L_y, and L_z are orbital angular momenta along x, y, and z directions, respectively.

The above equations reflect the fact that the orbital angular momenta along any two mutually orthogonal axes cannot be simultaneously measured with absolute precision unless the orbital angular momentum along the third axis (perpendicular to both other axes) vanishes. Pauli adopted similar commutation relations for the spin angular momentum operators, S_x, S_y, S_z

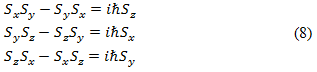
In Stern-Gerlach experiment, assuming z-axis is the axis joining the south to north pole of the magnet, the observation of two traces on the photographic plate was interpreted as being caused by a spin angular momentum S whose z-component has two values: ± ћ/2. Therefore, the matrix operator S_z should be (i) 2×2 matrix and (ii) Eigenvalues must be ± ћ/2. A 2×2 matrix that has the Eigenvalues of ± ћ/2 is the matrix