| |
5.3.4 Thermodyanamic Basis of Ferroelectric Phase Transitions
Thermodynamic theory to understand the ferroelectric phase transitions was developed after contributions from Lev Landau and V.L. Ginzburg, both Soviet physicists and A.F. Devonshire, British Physicist. The approach is based around calculating the free energy of system and working around other thermodynamic parameters to predict the nature of phase transition. Here, before we go into details of this theory, we will look at the some of the basic definitions.
These non-linear dielectrics exhibit various kinds of couplings between physical properties and can be expressed mathematically. For instance, below are the expressions for ferroelectric, piezoelectric and pyroelectric couplings.
Ferroelectric Effect:
Electric charge in a polar material can be induced by application of an external electric field and can be expressed as
where χij is the susceptibility in F/m (actually dimensionless but here εo i.e. permittivity of free space is also included which has dimension of F/m) and is second rank tensor. Note that the equation is valid only for the linear region of the hysteresis curve.
Piezoelectric effect:
Similarly, the charge induced by application of external stress i.e. piezoelectric effect, can be expressed by
where 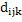 is the piezoelectric coefficient and is third rank tensor with units C/N, is the piezoelectric coefficient and is third rank tensor with units C/N, 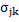 is the stress applied. is the stress applied.
Converse piezoelectric effect is expressed as
Where dijkt is in m/V.
Pyroelectric Effect:
Induced charge by temperature change i.e. pyroelectric effect is expressed by
where Pi is the vector of pyroelectric coefficient in cm-2K-1.
Displacement is expressed as
So, depending upon the state of material, many such effects may be present together. These couplings between thermal, elastic or electric properties can be understood formally by adopting a thermodynamic approach. The results of such an approach yield equations of state which relate the material parameters with different experimental conditions which assist in modeling of the parameters and in understanding the response of various devices.
From the laws of thermodynamics, the thermodynamic state of any crystal in a state of equilibrium can be completely established by the value of number of variables, which in case of ferroelectrics include temperature T, entropy S, electric field E, polarization P, stress s and strain e. Usually parameters like electric field E and stress s can be treated as external or independent variables while polarization and strain can be treated as internal or dependent variables.
For a ferroelectric system, the free energy G can be expressed in terms of ten variables as
where Px, Py, Pz are the components of the polarization, 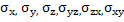 are the stress components and T is the temperature. are the stress components and T is the temperature.
We can get the value of the independent variables in thermal equilibrium at the free energy minimum. For an uniaxial ferroelectric, free energy can be expanded in terms of polarization ignoring the stress field. Here, we select the origin of free energy for a free unpolarized and unstrained crystal to be zero. Hence,
Note that only even powers are taken because energy is same for ±PS states.
Here a, b, c are the temperature dependent constants and E is the electric field.
The equilibrium is found by establishing 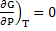 i.e. i.e.
i.e.
E = 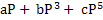 |
|
If all of a, b, and c are positive, then P = 0 is the only root of the equation as shown below in the figure. This is situation for a paraelectric material where polarization is zero when field is zero.
If we ignore higher power terms, then
leading to
which is the same expression that we encountered for linear dielectrics.
According to Landau-Devonshire theory, near the Curie point (T~T0) we assume
As a result, the free energy expansion (5.13), only ‘a’ is dependent on temperature while other constants are temperature independent. Incorporating (5.18) into (5.13) yields
In this expression, for all known ferroelectrics, both ao and c are positive while depending upon the sign of b, the phase transition nature changes.
Figure 5.6 (a) show the free energy vs polarization plot when T >> T0 i.e. when the crystal is in paraelectric state. On the other hand if, a < 0 when T << T0 and b and c are positive, there will be a nonzero root of P in addition P = 0, as shown below in figure 5.6 (b), representing the ferroelectric state with non-zero polarization at zero field.
| Figure 5.6 Free energy vs polarization for (a) paraelectric (above T0) and (b) ferroelectric crystal (below T0). |
|