5.3.3 Proof of Curie-Weiss Law
We can now say that in a ferroelectric material, reversible spontaneous alignment of electric dipoles takes place by mutual interaction. This happens due to a local field E' which is increased by dipole alignment in the direction of field. Interestingly, this phenomenon happens below a critical temperature Tc when crystal enters into nonsymetric state where thermal energy cannot randomize the electric dipoles, presumably due to dipole-dipole interactions and local field.
Following the basic principles we developed in module 4, polarization P can be expressed as:
Where local field E' = E + P/3ε0 as given by Clausius-Mossotti relationship and ε'r is the relative dielectric permittivity and α is total polarizability. Substitution for E' in (5.2) results in
i.e.
or
Since we know that susceptibility, 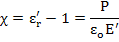 , we get , we get
Equation (5.4) shows that both χ and εr' must approach ∞ when Nα/3ε0 approaches 1.
This can be assumed to be a right condition for ferroelectrics as near the ferroelectric transition, they exhibit very large susceptibilities and dielectric constant. At this point, we can also ignore the electronic, ionic and interface polarizations assuming that dipolar polarizability is too high such that αd >> αe + αi + αint at a critical temperature Tc . Here define α = αd = C/kT where C is Curie’s constant. This is the right sort of relation as we have already seen the temperature dependence of dipolar polarization in section (4.5.3).
Hence, we can further write
OR
Below this Tc spontaneous polarization is prevalent and dipoles tend to align. So, since C = αdkT, we get
OR
Thus, by now modifying equation (5.4), Curie-Weiss law can be expressed as
|